科學,技術,工程和數學領域的師生
測量不確定度
什麼是測量?
測量是指為確定量測值而執行的一系列操作。
什麼是量測值?
對於通過測量而獲得的數量,我們有一個特殊的名稱。我們稱之為量測值。例如,如果我們使用電子天平來測量硬幣的質量,則硬幣的質量就是量測值。
什麼是測量不確定度?
測量結果由兩部分組成:一個稱為"測量值",另一個則稱為"測量不確定度"。
"測量值"是一個未知且不可知的值。它只是對量測值作出的估計。因此,所有的測量都存在不確定性,並且只有在同時給出測量值的不確定度的情況下,測量結果才是完整。
"測量不確定度"是指"測量值"的離散度,而此離散度可以合理地視為歸因於量測值。與上面的硬幣示例一樣,無論電子秤的質素如何,我們都只能說明硬幣的近似質量。因為在測量過程中有許多因素會影響測量結果,例如環境温度,壓力,等等。

如何量化測量值的離散度?
在統計學中,計算標準偏差是一種常用於量化一組數據的離散度的方法。
例如在一組含10個數值X1, X2, X3, X4, X5 … X10, 的測量中,其均值和標準偏差σ的計算如下。
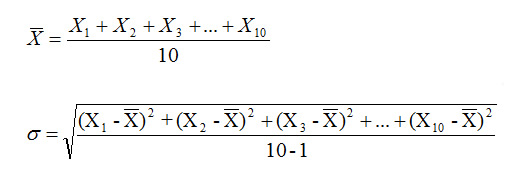
如何評估"測量不確定度"?
要了解如何評估測量不確定度,最好是用舉例說明的方法。以下是在電池電壓測量中評估測量不確定度的簡單示例。
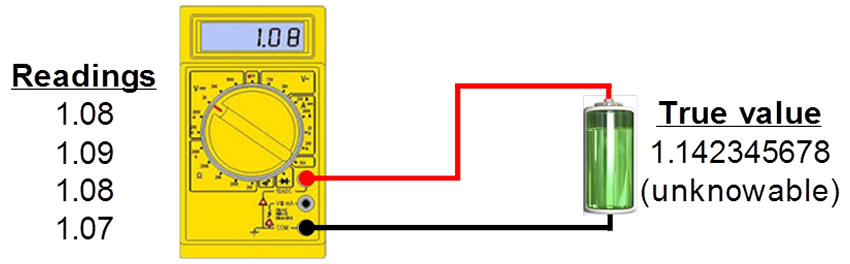
步驟1:定義量測值
量測值Y是電池的電壓,由電壓表測量。
步驟2:確定輸入參數並建立測量模型
可影響測量結果的輸入參數如下:
- M 電壓表的測量值
- R 由於電壓表的顯示分辨率而導致的不確定性
- A 對電壓表測量值的校正值
輸入參數(M,R和A)與測量值Y之間的數學關係稱為測量模型。示例如下:
Y = M + R + A
步驟3:評估每個不確定度來源的標準不確定度
對於每個輸入參數(也稱為不確定度來源),我們需要評估其標準不確定度。
- 標準不確定度 - 測量結果的不確定度,以標準偏差來表示。
以下有兩種方法可以評估輸入參數的標準不確定度,即A類和B類評估方法。
- A類評估方法以重複量測的數據所統計得來的標準偏差來評估不確定度的方法。
- B類評估方法利用非統計方法来获得標準不確定度。該標準不確定度一般是基於經驗或其他信息來直接給定的。
步驟3.1:評估電壓表測量值的標準不確定度M
在記錄了的四個電壓表讀數中(1.08 V,1.09 V,1.08 V,1.07 V),各個讀數的值皆有所不同。此乃由於每個影響測量值的參數均有一定的隨機性或隨機效應(例如環境温度的變化)。因此,使用A類評估方法來估計這種不確定性。這類評估方法是把測量值的平均值標準差(即實驗標準偏差)來作為其標準不確定度。以下是A類評估方法的示例:
先計算四個電壓表讀數的平均值M =(1.08 V + 1.09 V + 1.08 V + 1.07 V)/ 4 = 1.08 V,再計算其標準偏差及實驗標準偏差。

因此,M的標準不確定度為0.004082 V
步驟3.2:由電壓表的顯示分辨率R而導致的不確定性的評估
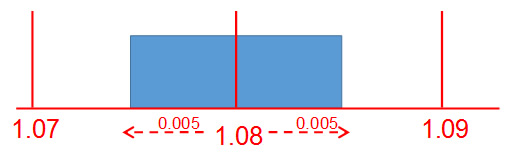
B類評估方法是用於估計由R而導致的標準不確定性。以下是B類評估方法的示例:
均值R為0,呈矩形分佈,其半寬為α = 0.005 V,則標準不確定度為:
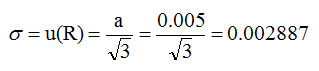
步驟3.3:評估對電壓表讀數的校正值A
A的值和標準不確定度皆由電壓表的校正證書所給出。假設校正證書指出電壓表的校正值為+0.06 V,擴展測量不確定度為0.04 V,覆蓋因子 k = 2。
對於A的標準不確定度所作出的B類評估為
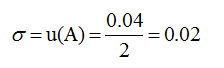
步驟4:推導合成標準不確定度
合成標準不確定度- 當一個測量結果由若干個其他量求得時,這個測量結果的標準不確定度,就等於這些其他量的方差或協方差之(加權)和的正平方根,稱之為"合成標準不確定度"。
在獲得所有參數的標準不確定度後,我們可以使用下面給出的不確定度傳播定律(LPU)來推導被測量項的合成標準不確定度。
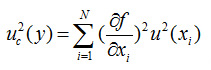
而 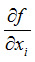 是靈敏度係數
是靈敏度係數
在此示例中,靈敏度係數為
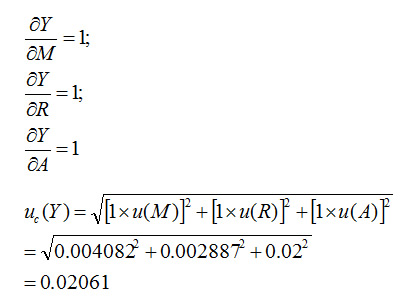
下表是該推導的總結。
| 不確定度來源 | 不確定度來源的數值 | 標準不確定度 | 概率分佈 |
|---|---|---|---|
| M | 1.08 | 0.004082 | 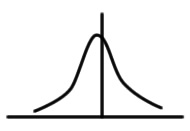 |
| R | 0 | 0.002887 | 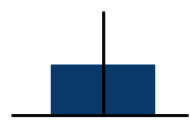 |
| A | 0.06 | 0.02 | 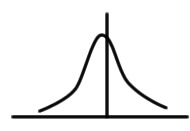 |
| Y | 1.14 | 0.02061 | 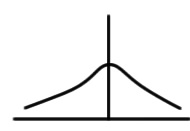 |
步驟5:評估擴展測量不確定度
- 擴展測量不確定度 U - 為了提高不確定度的置信水平,可將合成標準不確定度乘以一個數值因子k,由此得到擴展測量不確定度,它表示測量結果附近的一個置信區間,且可以合理地認為(或賦予)被測量值將以較高的置信概率落於該區間中;上述數值因子k通常稱為覆蓋因子。
- 覆蓋因子 k - 用作合成標準不確定度的乘數,以獲得擴展測量不確定度。
擴展測量不確定度U與它的覆蓋因子k, 表示被測量Y處於y-U到y+U的範圍內的置信水平為95%。擴展不確定度U由下式得出。
U = k×uc(Y)
覆蓋因子k的值取決於測量值的概率分佈。在“測量不確定度表示指南”的附件G中建議,在不違反中央極限定理的前題上,測量值可被視為遵循學生t分佈,其有效自由度Veff可從以下Welch-Satterthwaite公式來計算:
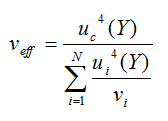
在這個例子中,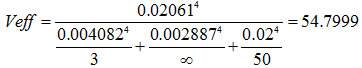 。從學生t分佈來看,有效自由度Veff為54.8的對應覆蓋因子值約為2.0049。因此,擴展測量不確定度 = 2.0049 × 0.02061 = 0.04132 ≈ 0.041。
。從學生t分佈來看,有效自由度Veff為54.8的對應覆蓋因子值約為2.0049。因此,擴展測量不確定度 = 2.0049 × 0.02061 = 0.04132 ≈ 0.041。
標準及校正實驗所測量不確定度軟件工具
標準及校正實驗所(SCL)開發出兩個軟件工具,即(i)「SCL Tool」和(ii)「SCL Simulator 不確定度評估模擬器」。前者根據《測量不確定度表示指南》(Guide to the Expression of Uncertainty in Measurement) (JCGM 100:2008)(又稱「GUM不確定度框架」),應用不確定度傳播定律,評估測量模型;後者則根據《測量數據的評估—測量不確定度表示指南補充文件第1號—使用蒙地卡洛法的分布傳播》(Evaluation of measurement data — Supplement 1 to the “Guide to the expression of uncertainty in measurement” — Propagation of distributions using a Monte Carlo method) (JCGM 101:2008),以蒙特卡洛方法(MCM)來模擬各種分布的傳播。兩個軟件工具均使用與EXCEL緊密結合的Visual Basic for Application (VBA)編程語言編寫而成,用戶可以簡單地在EXCEL工作表輸入測量模型和數值。
「SCL Tool」軟件工具
用戶可以為測量模型編碼,並在EXCEL工作表中以表格形式輸入相關的不確定參數(即參數值、標準不確定性和自由度)。該工具將自動計算靈敏度系數,並通過以下五個EXCEL用戶定義函數(UDF)輸出下列計算結果:
- 量測值 (UDF: gum_result() )
- 合成標準不確定度 (UDF: gum_csu() )
- 有效自由度 (UDF: gum_edof() )
- 覆蓋因子 (UDF: gum_k() )
- 擴展測量不確定度 (UDF: gum_eu() )
有關用於測量不確定度的SCL Tool的詳情,請參考這個軟件工具中各種測量模型的示例。
「SCL Tool」軟件工具(網頁版)
免責聲明
軟件工具由中華人民共和國香港特別行政區政府(下稱「政府」)轄下的標準及校正實驗所以「現況」形式提供,僅用作教育和一般參考用途。政府雖已盡力確保軟件工具所載資料準確,但政府對於有關資料的準確性、可用性、完整性、可靠性、是否適合作某特定或任何用途、安全性、適時性、所有權、是否侵權、適用性或效用,在香港特別行政區法律許可的範圍內,概不作任何種類(不論明示或隱含)的聲明、陳述、擔保或保證。對於任何因使用或不當使用、依據軟件工具的相關資料而引致或所涉及的任何損失、毀壞、損害、傷害或死亡(除非該等傷害或死亡是由政府或其任何僱員在僱用期間疏忽所致),政府概不承擔任何法律責任、義務或責任(包括但不限於疏忽責任)。
SCL模擬器
用戶可以表格形式指定相關的不確定參數(也稱為輸入參數),例如估算值、標準不確定度和概率分佈函數(PDF)等。SCL模擬器具備以下特點,用以設定MCM模擬模型:
- 多達八種適用於輸入參數的PDF賦值;
- 適用於相關輸入參數的多維高斯分布;
- 通過固定樣本數量或自適應模式選擇MCM試驗數量;以及
- 選擇對稱覆蓋區間或最短覆蓋區間進行不確定性評估。
MCM的模擬結果會顯示於同一張EXCEL工作表上。在自適應模擬模式中,SCL模擬器會按照補充文件第1號載列的方法自動檢查GUF的有效性。
有關SCL模擬器的詳情,講參閱軟件說明書及本模擬器中的測量模型編碼例子。
有關此軟件工具的查詢,請發送電子郵件至:hslam@itc.gov.hk
免責聲明:
- 本網站所載的資料由中華人民共和國香港特別行政區政府(下稱「政府」)轄下的標準及校正實驗所以「現況」形式提供,僅用作教育和一般參考用途。政府雖已盡力確保網站所載資料準確,但政府對於有關資料的準確性、可用性、完整性、可靠性、是否適合作某特定或任何用途、安全性、適時性、所有權、是否侵權、適用性或效用,在香港特別行政區法律許可的範圍內,概不作任何種類(不論明示或隱含)的聲明、陳述、擔保或保證。對於任何因使用或不當使用、依據相關資料或不能使用相關資料而引致或所涉及的任何損失、毀壞、損害、傷害或死亡(除非該等傷害或死亡是由政府或其任何僱員在僱用期間疏忽所致),政府概不承擔任何法律責任、義務或責任(包括但不限於疏忽責任)。
- 政府不保證或表示經由本網站傳送的任何資料不含電腦病毒。在使用本軟件工具或網站資料前,建議使用者先掃描電腦病毒。政府不會就本網站經互聯網傳送的資料而引致或所涉及的任何損失、毀壞或損害,承擔任何法律責任。
- 政府保留權利,按其絕對酌情權隨時略去、刪除、暫時停載或編輯由其編製的一切網站資料而無須給予任何理由或事先通知。使用者有責任自行評估本網站所載的各項資料,並在根據該等資料行事之前,加以核實(例如參照原本發布的版本)和徵詢獨立意見。
以下解釋標準及校正實驗所證書中的測量不確定度
示例:在標稱直流電壓10.000 V下校準電壓表
| Voltmeter | Measured Correction | |||
|---|---|---|---|---|
| Range | Meter Reading | Value y | Measurement Uncertainty | |
| Expanded Measurement Uncertainty U | Coverage Factor k | |||
| 10 V | 9.900 V | +100 mV | 1 mV | 2.0 |
如標準及校正實驗所證書所示,在儀表讀數為9.900 V時,測得的校正值y為+100 mV,擴展測量不確定度U為1 mV。這意味著校正值y處於從99 mV到101 mV的區間內的可能性大約為95%。當儀表讀數為9.900 V時,儀表測量的實際電壓將介於9.999 V至10.001 V之間,置信度約為95%。
 電壓表在10.000 V直流電壓下的校準示例
電壓表在10.000 V直流電壓下的校準示例
Reference
- Evaluation of Measurement Date – Guide to the Expression of Uncertainty in Measurement, JCGM 100:2008.
- Evaluation of measurement data – An introduction to the "Guide to the expression of uncertainty in measurement" and related documents, JCGM 104:2009
- International Vocabulary of Metrology – Basic and General Concepts and Associated Terms (VIM 3rd edition), JCGM 200:2012