科學,技術,工程和數學領域的師生
無處不在的計量學
質量
重力加速度在香港、赤道和南北兩極的故事

標準及校正實驗所
質量及力學實驗室
梁偉文、趙軍畧
A. 牛頓的萬有引力定律、萬有引力常數(big G)和重力加速度(little g)
如你讀過物理的話,你應該會知道艾碩牛頓提出行星和行星之間、月球和地球之間,以至樹上掉下來的蘋果,全部都受由他提出的「萬有引力定律」主宰。這個定律主張兩個質量之間的吸引力,是兩者質量的積除以彼此距離的二次方,再乘以萬有引力常數G。這道數式可顯示如下︰
 (1)
(1)
萬有引力常數G在英語中時常被稱為「Big G」,但它的數值是非常小,約為6.674 3 x 10-11 m3 kg-1 s-2,反映萬有引力比電磁力薄弱得多。以雪櫃上貼着的磁石紀念貼為例,整個地球的質量釋出的萬有引力,其實也比不過那塊磁石對雪櫃門所產生的磁力呢!
萬有引力常數「Big G」 與重力加速度「Little g」很容易令人混淆。重力加速度是指物體受地球的引力場影響而出現的運動加速度,根據牛頓運動第二定律,這股力量可顯示為算式(2)當中的mg,m即是物體的質量。
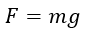 (2)
(2)
B. 引力加速度對計量學非常重要的原因
二十世紀前,測量重力加速度的主要目的是為了認識地球的形狀和了解地殼表面的質量分布。其後,測量重力加速度不單受大地測量師重視,對計量學家來說,測量重力加速度對力學、扭力和壓力亦尤其重要,這些測量利用已知質量在重力加速度下產生的重力作儀器校正。
B.1 產生已知力
就校正載荷感測器等力學測量儀器而言,力標準裝置是最準確的測量工具。在國際單位制中,力的單位是牛頓(N),力標準裝置產生的力(F)可從下列數式得出︰
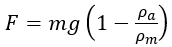 (3)
(3)


在數式中,m是所施加砝碼的質量,g是引力產生的重力加速度,ρm 和 ρa 則分別是砝碼和環境空氣的密度,而空氣密度ρa的數值只要使用由氣壓、温度和濕度的函數表示的近似公式進行運算便可得出[1][2]。
B.2 產生已知扭力
與測量力學相似,扭矩標準裝置是最能準確校正扭力感測器等扭力測量儀器的工具。
 圖2 在標準及校正實驗所的扭矩標準裝置
圖2 在標準及校正實驗所的扭矩標準裝置
在國際單位制中,扭力的單位是牛頓米(N.m),扭矩標準裝置產生的扭力(T)可從下列數式得出︰
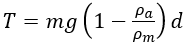 (4)
(4)
在數式中,m是所施加砝碼的質量,g是引力產生的重力加速度,d是扭矩軸中心和施加砝碼之間的距離。
B.3 產生已知壓力
氣體或液體活塞壓力計標準裝置都是測量壓力的常用標準,其運作原理是透過在精密活塞裝置的有效面積上施加已知質量的砝碼所產生的力來計算工作介質的壓力。


活塞壓力計標準裝置所產生的壓力P可從下列數式得出︰
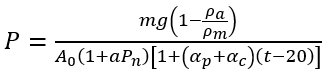 (5)
(5)
在數式中,m是所施加砝碼的質量,g是引力產生的重力加速度,ρa 和 ρm 分別是環境空氣和砝碼的密度,A0 是處於零壓力下的有效面積,a是活塞有效面積的失真系數,Pn 是等於mg/A0 的基本壓力, αp 和 αc 分別是活塞和汽缸的物料每攝氏度的線性熱膨脹系數,而t 則是活塞的温度。
C. 運用物理學估算g的數值
C.1. 基礎物理學中的g
要計算地球表面的g數值,看起來只需直接運用算式(1)和(2)即可。以一個蘋果為例,假設m1等於地球的質量(M ≈ 5.972 19 x 1024 kg),m2是蘋果的質量,r是蘋果與地心之間的距離,我們會得出︰
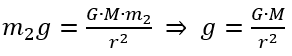 (6)
(6)
惟地球並非一個正圓球體,而是呈扁橢型的球體,因此r的數值在赤道會較南北兩極的半徑數值為大。從事地質測量學的科學家通常以橢球體代表地球的形狀,而其中廣為採用的橢球參數是WGS-84坐標系。雖然本文不會詳細說明WGS-84,但我們亦可把WGS-84的數據代入數式(6),看看在赤道、北極和本港標準及校正實驗所力學實驗室的g數值分別為何。結果列於表1。
不過,這些估值準確嗎?
| 位置 | 北極 | 赤道 | 香港 (力學實驗室) |
|---|---|---|---|
| 緯度 λ(度) | 90 | 0 | 22.314 84 |
| 與地心(WGS-84橢球參數)的距離(米) | 6 356 752.314 | 6 378 137 | 6 375 076 |
運用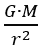 得出的g數值 得出的g數值 |
9.864 36 | 9.798 32 | 9.807 73 |
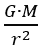 估算的g數值
估算的g數值
C.2. 國際重力公式
從事地質測量的人員時常會運用國際重力公式,用來計算某緯度為λ的位置的理論重力。這道公式能夠相當準確地估算出地球上不同地方的g數值。下列版本的公式是由Aziz 於2010年提出[3]︰
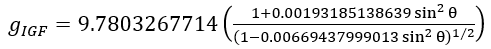 (7)
(7)
運用國際重力公式,便能得出赤道、北極和力學實驗室的g數值,結果載於表2。表1和表2的計算結果迥異,就北極所得出的數值相差達0.33%,原因是什麼呢?
| 位置 | 北極 | 赤道 | 香港 (力學實驗室) |
|---|---|---|---|
| 緯度 λ(度) | 90 | 0 | 22.314 84 |
| 運用國際重力公式得出的g數值 | 9.832 19 | 9.780 33 | 9.787 78 |
C.3. 影響g數值的其他因素
在推算數式(6)的過程涉及若干假設,其一是忽略地球自轉的影響,其二是假設兩個質量均為點質量。稍後讓我們看看這些因素對g數值有什麼影響。
C.4. 地球自轉對g的影響
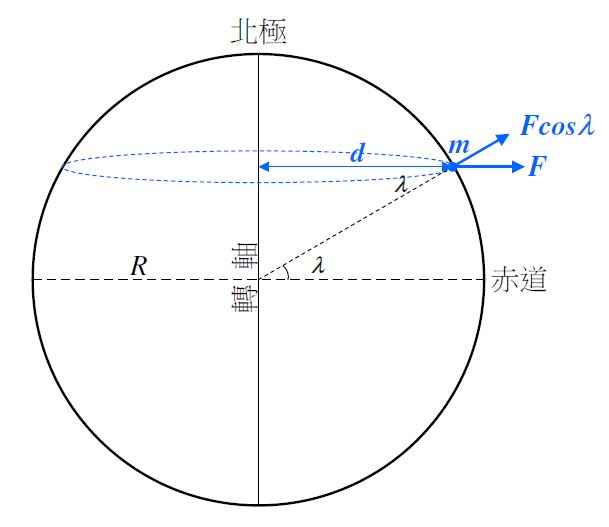
地球自轉對物體產生離心力,而離心力的強度取決於該物體的質量(m)、地球自轉速度(ω)的二次方,以及該物體與地球自轉軸的距離(d)︰
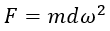 (8)
(8)
就處於緯度λ的物體而言,d等於r cos λ,r是該物體與地心之間的距離。離心力(F)屬外向力,並與自轉軸形成直角,而F與引力相對的組成部分為F cos λ。因此,引力對應地球自轉應按F cos λ的因子或者是 mrω2cos2λ減少,而 rω2cos2λ 則為g相應減少的數值,地球自轉速度ω值為7.292 115 x 10-5 rad s-1。
表3是表1的數據經修正後的結果。由此可見,地球自轉並不足以解釋表1和表2的結果之間的差異。
| 位置 | 北極 | 赤道 | 香港 (力學實驗室) |
|---|---|---|---|
| 緯度 λ(度) | 90 | 0 | 22.314 84 |
| 與地心(WGS-84橢球參數)的距離(米) | 6 356 752.314 | 6 378 137 | 6 375 076 |
(A) 運用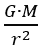 得出的g數值 得出的g數值 |
9.864 36 | 9.798 32 | 9.807 73 |
| (B) rω2cos2λ. (因地球自轉產生離心加速度的修正) |
0.000 00 | -0.033 92 | -0.029 01 |
| (A) + (B) | 9.864 36 | 9.764 41 | 9.778 72 |
C.5 因地球並非正圓球體而產生的影響
嚴格來說,數式(1)只適用於兩個質量點之間的情況。由於地球的質量並非集中於中心的某一點,因此數式(6)的結果僅為近似值。
假如一個物體的質量分布於某體積內,便可運用數式(1)計算該體積內所有質量的影響總和,從而得出在P點因該物體而產生的引力場。計算總和的過程涉及運用繁複微積分來解開拉普拉斯方程(Laplace Equation)和泊松方程(Poisson Equation),這兩道方程會在「附加說明」部分另作簡述,本部分只會論述相關結果。由於地球並非正圓球體,引力場涉及另一個根據緯度λ的程式項,這個程式項有時被稱為地球引力場的次級方程項,而其對g的影響表達如下:
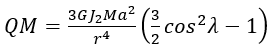 (9)
(9)
在數式中,J2是地球橢圓率的量度、M是地球的質量,而a是赤道半徑。J2採用大地测量参考系统的通用值為1.08263 x 10-3。我們把這次級方程項加入表3以得來獲得表4的計算結果,便會發現所得計算結果與國際重力公式的計算結果相當一致。
| 位置 | 北極 | 赤道 | 香港 (力學實驗室) |
|---|---|---|---|
| 緯度 λ(度) | 90 | 0 | 22.314 84 |
| 與地心(WGS-84橢球參數)的距離(米) | 6 356 752.314 | 6 378 137 | 6 375 076 |
(A) 由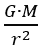 計算出的g數值 計算出的g數值 |
9.864 36 | 9.798 32 | 9.807 73 |
| (B) 因應地球自轉的離心加速度而作出的修正 | 0.000 00 | -0.033 92 | -0.029 01 |
| (C) 次級方程項 | -0.032 25 | 0.015 91 | 0.009 05 |
| (A) + (B) + (C) | 9.832 10 | 9.780 32 | 9.787 77 |
本部分適合高階程度的讀者,一般讀者可省略不看。下文會透過微積分解釋地球引力場的多極展開式。
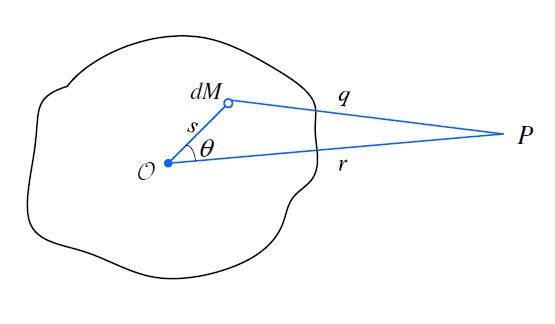
假如一個物體的質量分布於某體積(V)內,便可運用數式(1)計算該體積內所有質量(dM)的影響總和,從而得出在P點因該物體而產生的引力場。在這類問題中,先解開屬於非向量的引力勢(U(P))會較為容易。在P點因質量dM而產生的引力勢,可由GdM/q計算得出。在P點的總勢能如下:
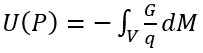 (10)
(10)
有一道廣為人知的數學公式說明了1/q與r、s和cosθ的關係,當中應用了著名的勒讓德多項式,包括P0(X) = 1、P1(X) = X,以及P2(X) = (3X2-1)/2等。
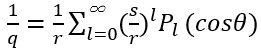 (11)
(11)
展開後便可得出:
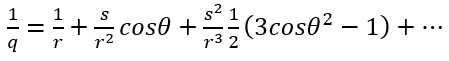 (12)
(12)
運用上述數式後,U(P)可展開為:
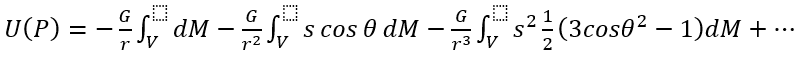 (13)
(13)
數式(13)右邊第一個項是初級方程項,進行積分後會變成-GM/r。就U(P)相對於空間坐標(r)進行微分後,便可得出重力加速度(GM/r2),這正正與針對兩個點質量的牛頓引力定律一模一樣。如果物體為均匀球體,在多極展開式中只有初級方程項並非零。
第二個項是次級方程項。如果物體的質量中心被選定為原點(O),次級方程項即為零。
第三個項是三級方程項(在多極展開式中此項亦會被稱爲四極距)。由於地球不是正圓球體,而是兩極扁平的扁橢圓球體,因此三級方程項並非零,其數值可在進行積分後按下列數式計算得出,並視乎r的方向而定。
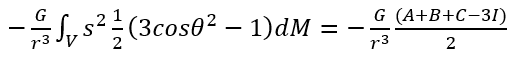 (14)
(14)
其中A、B、C和I分別是圍繞x、y和z軸及方向r的轉動慣量。假設地球的質量圍繞轉軸對稱分布,則A = B ≠ C,而I = A + (C-A) cos2θ。在大地測量學中,(C-A)通常會以J2Ma2表示,其中M是地球的質量,而a是赤道半徑。最後,適用於地球的數式(13)可簡化為下列數式:
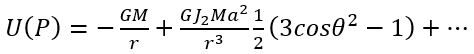 (15)
(15)
多極展開式還包括其他高階方程項(例如四級方程項和五級方程項等),惟其數值對地球的影響可忽略不計。
就U(P)相對於r進行微分後,便可得出以下的重力加速度:
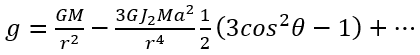 (16)
(16)
在地球上,θ是餘緯度並相等於(90°-λ),其中λ是緯度。若以緯度表示數式(16),便可得出:
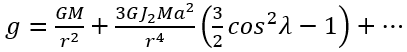 (16)
(16)
C.6 總論
總括來說,以下數式能有效估算在緯度λ的重力加速度g,準確度約為10-3。
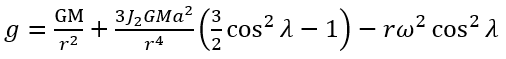 (17)
(17)
然而,對計量學的應用來說,該準確度並不足夠。g在某地點的實際數值,還取決於高度、地形、岩石密度、以及該地點周圍的地幔和地殼的不均勻性。為取得適合計量學應用的準確度,g的數值必須以重力儀測量進行實地測量。
D. 標準及校正實驗所在1990年以相對重力儀測量重力加速度
1990年7月,英國地質調查所(BGS)受前土木工程署轄下的土力工程處委託,在中國香港和隸屬前工業署的標準及校正實驗所展開一項關於引力的大型調查[4][5]。
英國地質調查所在1990年進行有關調查時,採用了屬於相對重力儀的拉–羅氏G型重力儀,其讀數準確度最高達1 x 10-7 米/平方秒。當時,這種重力儀是1971年國際重力標準網(IGSN71)所採用的主要儀器,而該標準網屬於全球性網絡,亦是絕對重力測量的參考標準框架[6]。
中國香港在1970年代共設有十個IGSN71基站,直至1990年僅餘三個。英國地質調查所在1990年進行有關調查,重新確認餘下三個基站的一致性,並設立四個新基站。調查期間,英國地質調查所在全港18個不同地點(例如在香港島香港大學的科學館、九龍李鄭屋漢墓的入口、大嶼山的梅窩警署,以及新界大帽山的三角測量站等),進行共71 次重力觀測,測量所得的重力加速度介乎9.785 398 5 米/平方秒至9.787 624 9 米/平方秒。
1990年7月5日和6日,英國地質調查所分別在標準及校正實驗所轄下位於九龍灣分所的力學實驗室和位於灣仔入境事務大樓總所的質量實驗所,進行實地重力測量工作。由英國地質調查所提供測量所得的重力加速度摘錄於表5,測量的不確定度為5 x 10-7米/平方秒。
| 地點 | ||
|---|---|---|
| 九龍灣力學實驗室 地下 |
灣仔入境事務大樓35樓 質量實驗室 |
|
| 測量所得的重力加速度(米/平方秒) | 9.787 601 5 | 9.787 234 6 |
E. 標準及校正實驗所在2019年以絕對和相對重力儀測量重力加速度
標準及校正實驗所沿用了英國地質調查所所提供的重力數值超過25年。隨着分所和總所周圍的環境經歷種種變遷,加上技術評審專家提出建議,標準及校正實驗所認為重新測量重力數值實屬必要,遂於2019年2月委託數位來自中國計量科學研究院(NIM)的專家,前往位於九龍灣的力學實驗室和位於灣仔的質量實驗所、振動實驗所和壓力實驗所,對重力加速度進行實地測量。
力學實驗室設置了由中國計量科學研究院研發的NIM-3A型[7]高精度絕對重力儀。該重力儀所測量的重力數值會作為參照基準,其運作原理是在真空管內掉下一個物體,然後以激光干涉儀測量該物體掉落一段指定距離所需的時間[8][9]。接受測試的質量的加速度可根據測定的掉落軌跡直接計算得出,然後以相對重力儀測量在質量實驗所、振動實驗所和壓力實驗所的重力數值。

圖4 用於測量在力學實驗室的重力加速度的絕對重力儀

圖5 用於測量在質量實驗室、振動實驗室和壓力實驗室的重力加速度的相對重力儀
中國計量科學研究院專家測量所得的重力加速度摘錄於下表,測量的不確定度在5 x 10-7 米/平方秒之內。
| 地點 | ||
|---|---|---|
| 九龍灣力學實驗室 地下 |
灣仔入境事務大樓35樓 質量實驗室 |
|
| 測量所得的重力加速度(米/平方秒) | 9.787 600 5 | 9.787 235 2 |
F. 對比g在力學實驗室實地測量的數值與理論上的估算值
對比g的實地測量數值與理論上的估算值,結果相當有趣,有關數據載於表7。我們觀察到,從數式(6)計算得出的數值與2019年在力學實驗室實地測量的數值相差0.21 %。考慮到因地球自轉,以及其並非正圓球體而產生偏差等因素而作出修正後,有關偏差減至0.002 %。
| 香港 (力學實驗室) |
|
|---|---|
運用數式(6)由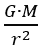 計算得出的g數值 計算得出的g數值 |
9.807 73 |
運用數式(17)由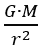 計算得出,並因應地球自轉和四極矩而作出修正後的g數值 計算得出,並因應地球自轉和四極矩而作出修正後的g數值 |
9.787 77 |
| 運用數式(7)由國際重力公式計算得出的g數值 | 9.787 78 |
| 英國地質調查所專家在1990年實地測量的數值 | 9.787 601 5 |
| 中國計量科學研究院專家在2019年實地測量的數值 | 9.787 600 5 |
牛頓的萬有引力定律適用於所有物體。不過,推算數式(6)的過程涉及若干假設,其一是假設兩個質量均為點質量,即代表其幾何尺寸並不重要。此外,地球是扁橢圓球體而非正圓球體,密度並不均勻,質量分布也不一致,並會持續自轉。另外,g的數值會隨着高度的增加而按每米3.086 x 10-6的比率(約每米-0.000 031 5%)下降。上述所有因素均可用來解釋g的測量數值與估算值之間的偏差。
參考資料:
- Davis, R.S., “Equation for the determination of the density of moist air” (1981/91), Metrologia 29, 67 (1992).
- Giacomo, P., “Equation for the determination of the density of moist air” (1981), Metrologia 18, 33 (1982).
- Aziz, N., Majid, B. and Jorg, E. (2010), “Gravity and Magnetic Data Acquisition Over a Segment of the More-Trondelag Fault Complex”, NGU Report 2010.049.
- EVANS R B (1990). Hong Kong gravity observations in July 1990 with BGS Lacoste and Romberg meter No. G97 and international connections to IGSN 71. British Geological Survey Technical Report WK/90/24R.
- Busby, J.P., Evans, R.B., Lam, M.S., Ridley Thomas, W.N. & Langford, R.L. 1992. The gravity base station network and regional gravity survey of Hong Kong. Geological Society of Hong Kong Newsletter, Vol. 10, pp 2 - 5.
- C. Morelli, C. Gantar, T. Honkasalo, R.K. McConnell, J.G. Tanner, B. Szabo, U. Uotila, C.T. Whalen, The International Gravity Standardization Net 1971. Special Publication No 4 of the International Association of Geodesy, 1974.
- Wu Shu-qing, Feng Jin-yang, Li Chun-jian, Su Duo-wu, Wang Qi-yu and all the participants, CCM.G-K2.2017 CIPM Key Comparison of Absolute Gravimeters, Metrologia, Volume 57. Number 1A (2020).
- Li Chun-jian, Xu Jin-yi, Feng Jin-yang, Su Duo-wu, Wu Shu-qing, Correction of NIM-3A absolute gravimeter for self-attraction effect. Ninth International Symposium on Precision Engineering Measurement and Instrumentation, 2015
- Shuqing Wu, Tianchu Li. Technical Development of Absolute Gravimeter: Laser Interferometry and Atom Interferometry[J]. Acta Optica Sinica, 2021, 41(1): 0102002(in chinese)吳書清, 李天初. 絕對重力儀的技術發展: 光學干涉和原子干涉[J]. 光學學報, 2021, 41(1): 0102002
光學及輻射度
智能電話能否作測光之用?

標準及校正實驗所
光度及輻射度實驗所
李河堂 林凱珊
1). 引言
智能電話內置各式各樣的感應器,為電話系統提供不同的功能。電話程式開發者亦在研發的過程中注入創意元素,利用這些內置感應器開發出各種新穎有趣的流動應用程式。測光錶應用程式就是其中一種用於攝影或照明設計的流動應用程式,聲稱能利用智能電話提供簡易、方便的光照度測量。市面上有多款測光錶應用程式,但這些程式能否準確測量光照度?或者說,它們測量的物理量,是否正是光照度呢?
測光錶用於測量光照度,而光照度是指每單位面積接收到的光通量(lm/m2) [4]。光照度的物理表達式為
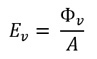
其中Ev是光照度,A是探測器所涵蓋的測量面積,而Φv則是在面積A所接收到的光通量。光照度的國際單位制(SI)單位是勒克斯(lux, 符號為lx),因此測光錶又通稱為光照度計/勒克斯計。
光通量(單位:流明(lumen, 符號為lm))是光度學的量,為光源輸出的總光量,與正常人眼睛對不同波長輻射的感光度相關。在一般情況下,光源於球面範圍S1和球面範圍S2(見圖F1)內的總光通量相同。一個涵蓋測量面積A的探測器在兩個不同距離r1和r2的位置上所接收到的光通量,會按照總光通量的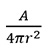 比率(即
比率(即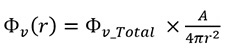 )而有所不同。因此,光照度會遵從著名的平方反比定律,與1/r2成正比:
)而有所不同。因此,光照度會遵從著名的平方反比定律,與1/r2成正比:
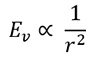
 圖F1. 應用於光照度的平方反比定律。A是探測器所涵蓋的測量面積。
圖F1. 應用於光照度的平方反比定律。A是探測器所涵蓋的測量面積。
2). 傳統測光錶
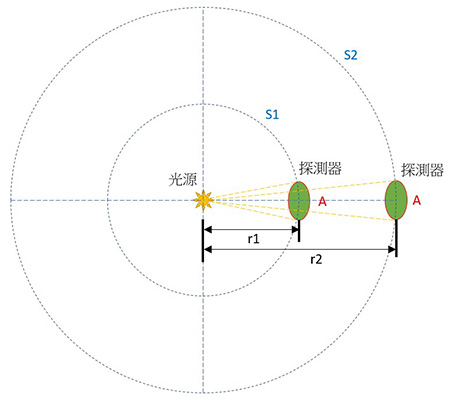
測光錶是光度學上測量光照度的工具。光照度的SI單位為勒克斯(符號:lx),即等於每單位面積接收到的光通量(lm/m2)。照度計的傳統設計載於圖1,它有三個主要組件,分別是一個餘弦散光器、一個光度函數濾光鏡(或稱V(λ)濾光鏡),以及一個光電二極體。
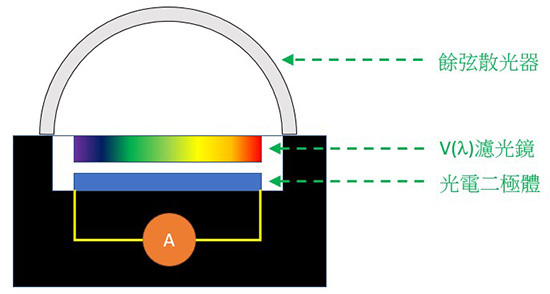 圖1. 測光錶的主要組件
圖1. 測光錶的主要組件
測量光照度時,光照強度遵從朗伯餘弦定律(見圖2),與光源入射角的餘弦成正比。一般來說,外來光線並非全部垂直照入目標區域。餘弦散光器是根據不同入射角度為光照度測量作出餘弦修正的組件。以圖3所示的房間環境為例,人對房間「表觀亮度」的感知,會受到多重光源及從不同角度而來的環境反射光所影響。因此,餘弦散光器會以不同角度收集光線,以模擬眼睛對四周環境的反應。
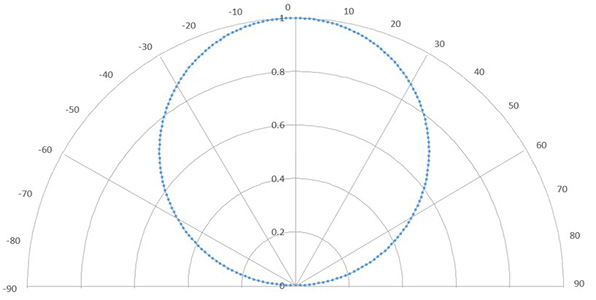 圖2. 朗伯餘弦定律
圖2. 朗伯餘弦定律
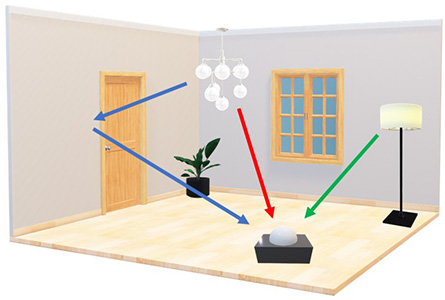 圖3. 房間環境的光照度
圖3. 房間環境的光照度
V(λ)濾光鏡是一個帶通濾光鏡,在可見光譜中具有不同的光譜透射比,特別為配合光電二極體的電氣特性而設,以提供與圖4所示人眼明視覺響應的光譜光視效率函數(或稱V(λ)函數)匹配的整體相對光譜響應度[1]。人的視覺只能看見可見光譜(波長約介乎約380納米至780納米之間[1]),並對「綠色」(波長約555納米)最為敏感,對藍光和紅光波長區域的敏感度較低,而對紫外光和紅外光則沒有反應。不過,硅探測器等光電二極體能對包括可見光譜、紫外光以至紅外光範圍的廣闊光譜作出反應。因此,V(λ)濾光鏡旨在阻隔紫外光和紅外光,並提供與人眼的V(λ)函數匹配的整體光譜響應度。測光錶中的光電二極體會匯聚所有屬可見光譜範圍內的光線,然後產生以安培(A)為單位的輸出電流,其數值與勒克斯值成正比。當我們得知光電二極體的光照度響應度(A/lx)後,便可測量光照度的數值。
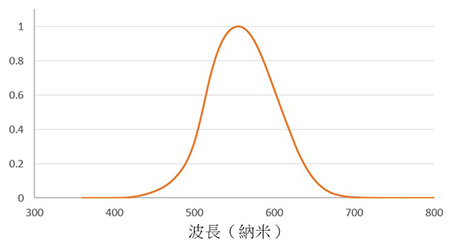 圖4. 人眼的光視效率(V(λ))函數
圖4. 人眼的光視效率(V(λ))函數
光透射比是指光線穿過表面時的透射光輻射和入射光輻射之比。舉例來說,製造防藍光玻璃時可加上反光塗層,一方面反射紫外光以至藍光,另一方面讓其他波長的光線通過(如圖F1所示)。
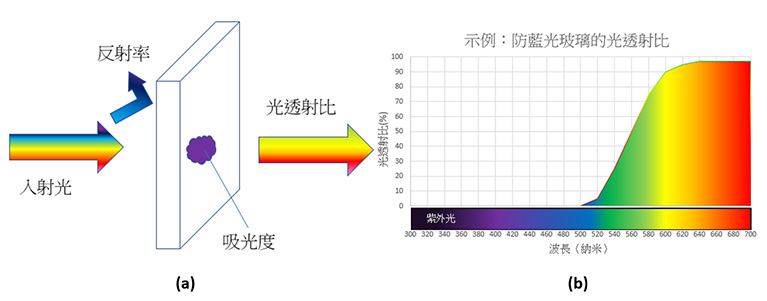 圖F1.(a) 光透射比、反射率和吸光度;(b) 防藍光玻璃的光透射比
圖F1.(a) 光透射比、反射率和吸光度;(b) 防藍光玻璃的光透射比
3). 智能電話使用的測光錶應用程式
圖5是智能電話使用的測光錶應用程式示例,使用者可利用智能電話內的相機或環境光感測器測量「勒克斯值」。
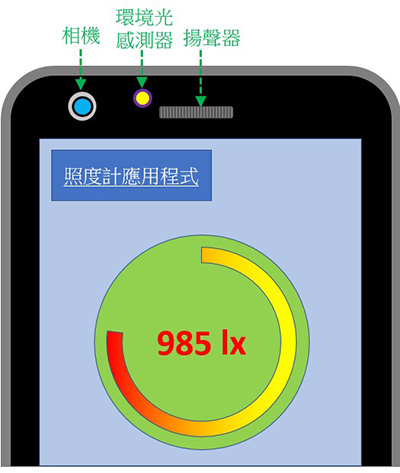 圖5. 測光錶應用程式示例
圖5. 測光錶應用程式示例
智能電話使用的測光錶應用程式主要有兩種,分別有利用環境光感測器和由相機作為光檢測器。第一種(下稱「環境光感測器型測光錶應用程式」)較常見於使用安卓(Android)作業系統的電話,當中的環境光感測器開放予軟件開發者使用;而iPhone電話則不鼓勵開發者使用環境光感測器,凡使用這種感測器的應用程式均未能在App Store應用程式商店獲得批准上架。這項限制令多數為iPhone而設的測光錶應用程式只能選用相機作為iPhone的光檢測器,這種程式下稱「相機型測光錶應用程式」。
智能電話的相機在變焦和成像方面的光學設計較為複雜,惟設計專為攝影而設,並非用於測量光照度。在使用環境光感測器與相機作為光檢測器時,兩者之間的主要差別如下:
- 環境光感測器直接測量光照度。
使用環境光感測器測量光照度時,應將其放在面向光源的目標區域。 - 相機測量目標區域的亮度(在光度學而言,亮度和光照度是兩個不同的物理量)。
測量目標區域的光照度時,相機會拍攝該區域的影像以測量亮度,並透過假設該區域的反射率來把亮度換算成光照度。
由於相機型測光錶應用程式在估算目標區域反射率時的不確定度較大,其準確度較環境光感測器為低,故下文將不再作深入討論,而會集中探討以環境光感測器進行的測量。
亮度通常指目標區域的光暗度。正式的定義是:在特定方向上某特定點的亮度(Lv),是指每單位球面度(sr)和每單位投影面積(m2)垂直於指定方向的光通量(lm),其測量單位為lm/sr/m2 [4]。
相機檢測的物理量是目標區域的亮度。
相機感應器如何測量光照度?
相機通常會從有限的角度對焦目標區域並構成影像,然後測量目標表面反射光的光通量「密度」。如輻射功率或目標與光源之間的距離不變,目標區域的光通量「密度」亦會維持不變。因此,即使相機與目標表面之間的觀察距離改變,相機仍會自動重新對焦該表面而得出相同的亮度結果。
圖F2闡述相機如何估算光照度。光源照射目標區域的光照度是Ev,目標表面的反射亮度將會聚焦於相機感應器上作檢測,其強度取決於目標區域的光照度Ev和目標表面的反射率R。之後,相機會透過假設反射率(例如基於過往的測試狀況[5])來得出光照度。由於這個方法在估算目標區域反射率方面的不確定度較大,因此測量光照度的準確度較低。
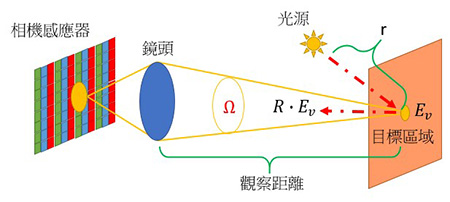 圖F2. 目標區域在相機感應器上的成像。光源在距離r下照射目標。假設照射分布均勻,Ev是目標區域的光照度,R是有關表面的局部反射率,而Ω則代表觀察系統的角度。
圖F2. 目標區域在相機感應器上的成像。光源在距離r下照射目標。假設照射分布均勻,Ev是目標區域的光照度,R是有關表面的局部反射率,而Ω則代表觀察系統的角度。
實驗
圖F3是一項簡單實驗,利用傳統儀器級別的測光錶和安裝了相機型測光錶應用程式的智能電話來量度目標表面的光照度,從中展示目標區域的反射率對有關應用程式讀數的影響。相機型測光錶應用程式因應反射率不同的目標表面,錄得的光照度讀數差距甚大-黑色背景錄得38 lx,白色背景錄得159 lx;傳統測光錶的讀數則較為一致,約為256 lx。
 圖F3(a)利用智能電話相機作為反射式測光錶進行實驗;以相機測量(b)黑色表面和(c)白紙錄得的光照度讀數。傳統照度計的讀數約為256 lx。
圖F3(a)利用智能電話相機作為反射式測光錶進行實驗;以相機測量(b)黑色表面和(c)白紙錄得的光照度讀數。傳統照度計的讀數約為256 lx。
環境光感測器原用作探測智能電話的入射光強弱,從而自動調節屏幕的光暗度。圖6顯示典型環境光感測器的組裝設計圖。智能電話的屏幕下設有內置的環境光感測器晶片(其透光孔面積較細),晶片一般配備濾光鏡用以感應可見光,並可能附有與環境光感測器晶片一同生產或裝配的模製透鏡,以加強光耦合作用。圖7說明傳統測光錶與智能電話環境光感測器在受光角度方面的分別。傳統測光錶凸出的餘弦散光器設計能以較大的入射角度接收外來光;相反,內置式的環境光感測器設計令受光角度有所局限,在多重光源的環境下難以量度出準確的餘弦修正結果(例如圖7所示的感應器便不能接收紅線表示的光線)。
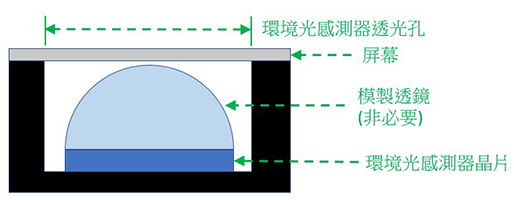 圖6智能電話環境光感測器的典型組裝設計圖
圖6智能電話環境光感測器的典型組裝設計圖
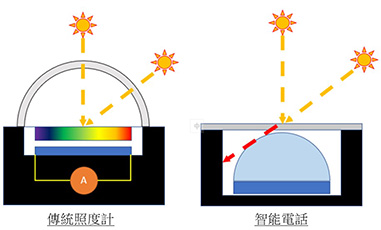 圖7 來自不同角度的入射光
圖7 來自不同角度的入射光
測量光照度的另一個關鍵元素是能與V(λ)函數匹配的響應度。圖8展示三款坊間常見的環境光感測器感應晶片,其光譜響應度資料來自其數據手册。
圖8(a)中的環境光感測器(下稱「A類」)配備四個分別可響應紅色、綠色、藍色和白色光譜的光電二極體,這類環境光感測器亦可附有用於多重顏色感應的高光譜感應器陣列。這款環境光感測器晶片或其軟件推動程式會對三原色感應器或白色感應器的感應電流分配不同的加權因子,用以計算「勒克斯」的數值。智能電話相機的影像感應器, 配備多組三原色感應器(或像素), 便類似這種環境光感測器。例如,三原色感應晶片可應用加權算式「(0.2126*R) + (0.7152*G) + (0.0722*B)」[2, 3],從「紅(R)」、「綠(G)」、「藍(B) 」顏色像素的輸出水平計算出光照的強弱。
圖8(b)是雙頻式環境光感測器(下稱「B類」),它配備一個寬帶感應器和一個紅光至紅外光感應器。B類光感測器會先計算兩個感應器的輸出電流的差額淨值,再乘以修正因數來估算「光照度」的數值。
而圖8(c)則展示另一款環境光感測器(下稱「C類」),其光譜響應度與發光效率函數十分接近。
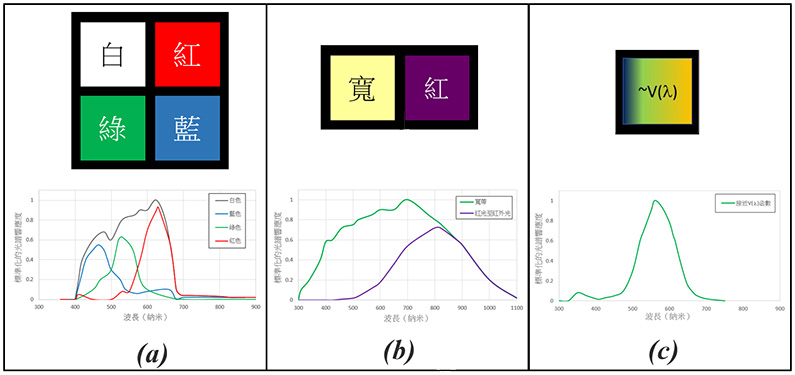 圖8 環境光感測器晶片的常見類型((a)A類、(b)B類、(c)C類)
圖8 環境光感測器晶片的常見類型((a)A類、(b)B類、(c)C類)
圖9是上述三款常見的環境光感測器的標準化光譜響應度與V(λ)函數的比較,其中曲線(a1)是在可見光譜內有一條通帶的A類白光感應器的光譜響應度;曲線(a2)是A類三原色感應器經過加權算式「(0.2126*R) + (0.7152*G) + (0.0722*B)」運算後得出的光譜響應度;曲線(b)是B類設計從寬帶感應器減去紅光至紅外光感應器反應後得出的光譜響應度淨值;而曲線(c)則是C類設計的光譜響應度。圖9的圖表顯示,A類和B類設計(即曲線(a1)、(a2)和(b))的光譜響應度與V(λ)函數差異甚大, 其中B類設計在測量中吸收過量紫外光和紅外光,而C類設計則與V(λ)函數較為吻合。不過,C類設計的濾光鏡透射譜向紅光偏移,且在紫外光波長範圍出現一個細小的透射波峰,因此C類設計的濾光鏡質素仍有改善空間。
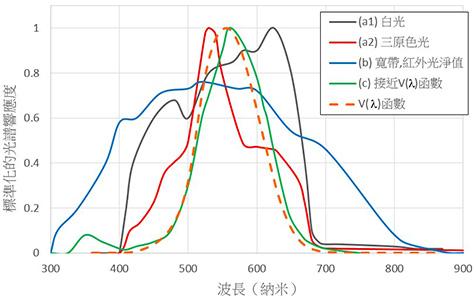 圖9 A類至C類環境光感測器的標準化光譜響應度與V(λ)函數的比較
圖9 A類至C類環境光感測器的標準化光譜響應度與V(λ)函數的比較
4). 討論
從第3部分可見,智能電話內置的環境光感測器受其裝配設計所限,未必能夠提供良好的餘弦修正光照度測量結果,而各款環境光感測器晶片的光譜響應度亦差異甚大,未必能夠達到良好的V(λ)匹配反應。為進一步了解光譜錯配的影響,我們就A類感應器的光譜響應度與LED燈和鎢絲燈的光譜功率分布進行比較(見圖10)。
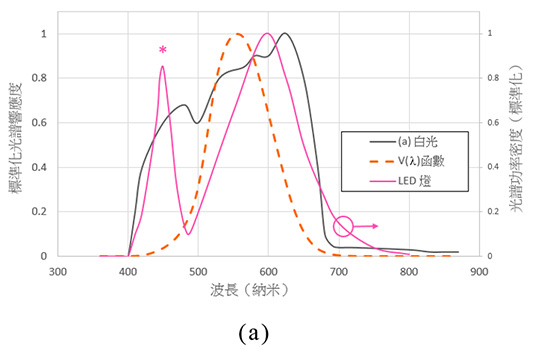
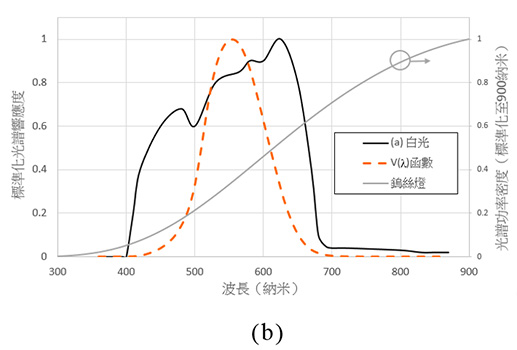
在兩種情況下,A類白光感應器在藍光區(波長約為400納米至500納米之間)和紅光區(波長約為600納米至680納米之間)接收到的燈光功率均較高。例如,圖10(a)中LED燈的藍光波峰頂點(*)會成為環境光感測器的其中一大電流輸出來源,導致光照度測量結果產生錯誤。再者,不同型號的智能電話亦可能內置了不同的環境光感測器晶片,即使利用相同的測光錶應用程式,勒克斯讀數仍會受不同型號的智能電話內的光感測器影響,使用者或難以知曉光照度測量結果的準確性。
綜合以上討論,雖然智能電話的測光錶應用程式能提供十分方便的測光方法,惟使用者如重視光照度測量結果的準確性,便須留意這種測量系統的各種局限。
參考資料︰
[1] ‘Illuminance meters – Requirements and test methods’, British standard BS 667:2005.
[2] ‘Smartphone-Based Light Intensity Calculation Application For Accessibility Measurement’, N. Negar et al., RESNA ANNUAL CONFERENCE – 2014.
[3] ‘Why You Should Forget Luminance Conversion and Do Something Better’, Rang M. H. Nguyen et al., 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR).
[4] ‘Handbook of applied photometry’, C. DeCusatis; Optical Society of America, 1997
[5] Estimating luminance and illuminance with reflection-type exposure meters and an 18% neutral test card, Kodak, 1999
時間及頻率
在中國香港不同的地方,時間的流逝速度會有不同嗎?

標準及校正實驗所
先進通訊技術實驗所
歐陽頌輝博士、楊承隆博士
國際單位制的時間單位為「秒」(s),是通過銫頻率ΔvCs的固定數值來定義。銫頻率指銫133原子在不受干擾基態的超精細能階躍遷頻率,頻率值為9 192 631 770 Hz。
標準及校正實驗所負責為香港維持時間和頻率的參考標準,自1986年起便利用銫原子鐘來實現國際單位制的秒,目前採用的銫原子鐘準確度達8 x 10-14,即每40萬年誤差僅約為1秒。
 圖1:標準及校正實驗所的銫原子鐘
圖1:標準及校正實驗所的銫原子鐘
「時間」在物理學上具有深層意義。很多人都曾聽過愛因斯坦的相對論,當中主張時間並非絕對。這引申出一個深奧的問題 — 時間在中國香港不同的地方會有相同的流逝速度嗎?倘將銫原子鐘放在(a)星光大道或(b)大帽山山頂,銫原子鐘量度的時間是否一樣?
 (a)
(a)
 (b)
(b)
要回答這個問題,先要更深入了解愛因斯坦的理論。相對論實際上有兩種,分別是狹義相對論和廣義相對論。愛因斯坦在1905年發表了狹義相對論,提出時空這個新概念。三維空間與一維時間共同構成四維時空。時間並非絕對,而是會隨着觀察者和時鐘的參考系的相對運動而變化。簡單來說,在觀察者眼中,移動中的時鐘會走得慢了,這就是以洛倫茲變換命名的洛倫茲時間膨脹。洛倫茲變換涉及兩個相對以均速運動的慣性系時空坐標之間變換的關係。
即使在觀察者和時鐘彼此相對上皆是靜止不動的情況下,仍可發生時間膨脹現象。愛因斯坦早在1915年發表的廣義相對論中,已對另一種時間膨脹現象,即引力時間膨脹作出預言。
1905年以後,愛因斯坦發現部分公認的物理學理論,包括牛頓的引力理論,與狹義相對論並不一致。為解決兩者的不一之處,愛因斯坦提出廣義相對論,對引力提出截然不同的觀點。根據牛頓的理論,引力是物體之間因質量而產生的吸引力;而在愛因斯坦的理論中,引力是大質量物體造成時空彎曲所產生的結果(圖3)。
 圖3. 時空曲率
圖3. 時空曲率
簡單來說,物質(廣義上包括質量、能量和動量)會扭曲周圍的四維時空,在彎曲的時空中移動的其他物體,便會顯得受一股稱為引力的力量所影響。
在廣義相對論中,著名的愛因斯坦場方程式闡述了時空幾何與物質分布的關係。
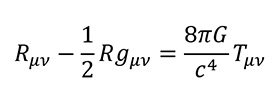 (1)
(1)
這個張量方程式涉及高階數學,本文只能稍作介紹。參數Rµν、R和gμν代表時空曲率,而Tµν,(稱為能量-動量張量)則代表大質量物體的影響。G是引力常數,而c則為光速。
由於大質量物體會扭曲周圍的時空,因此作為四維時空其中一項元素的「時間」便會視乎引力場的強度,以不同的速度流逝。這就是引力時間膨脹的基礎。綜上所述,引力場愈強,時鐘便運行得愈慢。
要計算引力時間膨脹的影響,可以運用以下從史瓦西對愛因斯坦場方程式的解法推導出來的方程式計算。
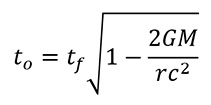 (2)
(2)
其中:
G是引力常數 (6.6743 x 10-11牛頓平方米/平方公斤)
M是產生引力場的質量
r是物體與質量中心之間的距離
c是真空中的光速 (299792458米/秒)
tf是參考觀察者於距離為無限遠時的時間流速
to是物體與質量之間的距離為r時的時間流速
地球的質量(M)約為5.9722 x 1024公斤;在中國香港,地球的半徑(r)約為6.375 x 106米。
現在讓我們回到問題:時間在星光大道和在大帽山山頂是否以同等速度流逝?要得知答案,先要知道這兩個地方的高度。
星光大道: 5米*
大帽山: 957米*
*由「香港主水平基準」向上計算,其基準處於「平均海平面」以下約 1.3 米。
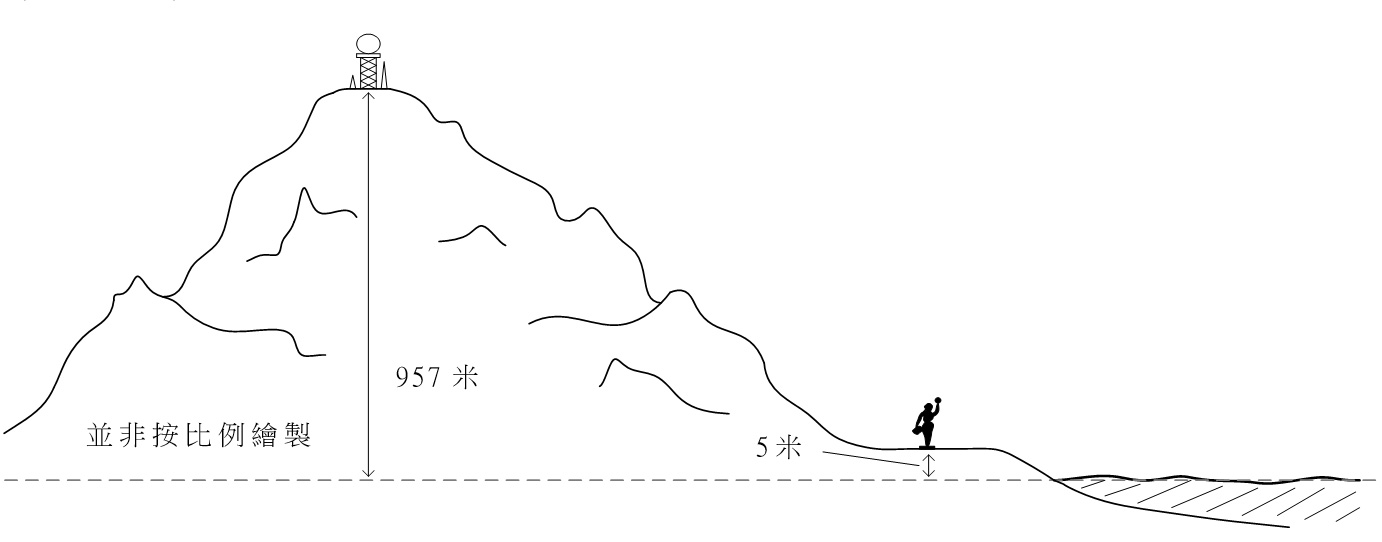 圖4. 時間在不同高度的流速
圖4. 時間在不同高度的流速
接着,我們可以運用方程式(2),計算物體在星光大道(taos)和大帽山山頂(ttms)的時間流速︰
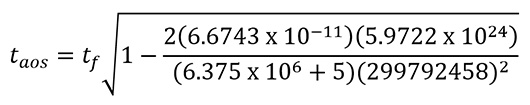 (3)
(3)
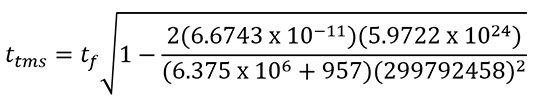 (4)
(4)
ttms與taos的比率如下︰
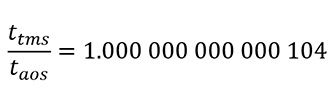 (5)
(5)
計算結果顯示,原子鐘在大帽山山頂上運行的速度,較在星光大道快約1.000 000 000 000 104倍。由於一天有86 400秒,因此將原子鐘由星光大道移往大帽山山頂,原子鐘每日便會運行快約9納秒 (9 x 10-9 s)。
不過,引力時間膨脹只會影響最精準的原子鐘。以地球表面計算,每昇高1米便有約1016分之一的相對時間膨脹差異,但這種差異對一般時間和頻率測量儀器的影響可說是微不足道。
愛因斯坦在1915年發表場方程式後不久,史瓦西便發現了於球形質量外圍的引力場的精確解。
假如沒有引力場,時空是平坦的,兩件事件之間在球面坐標的距離(ds)可以用下列方程式表達:
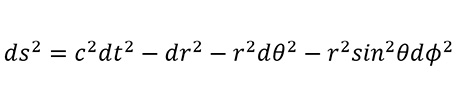 (6)
(6)
史瓦西發現,在有球形質量M的情況下,時空會遵循愛因斯坦場方程式而扭曲。上述方程式會變成下列方程式,又稱為史瓦西度規。
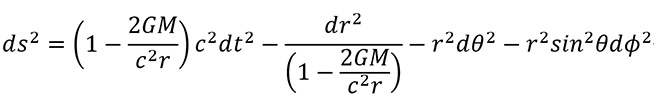 (7)
(7)
計算引力時間膨脹的方程式可從史瓦西度規直接得出。
與我的11歲兒子暢談量子物理學
(第1部分:原子鐘和銫-133原子的超精細能階躍遷)

黎孝華博士
射頻實驗室
標準及校正實驗所
一天晚上約9:30
爸爸,可以說一個故事給我聽嗎?
沒有問題,等一秒(等一下)吧!
我現在可以了,你現在可以嗎?
是的,我準備好了。我已經等了您很多秒!您的一秒鐘真是太長!我們是否活在一個平行時空?
哎,請不要嘲笑爸爸,我需要完成手頭上的工作。我知道你最近的數學課正好是學習關於時間的單位換算,就讓我說一個關於秒的故事吧。
關於秒的故事?聽起來很有趣,我從來沒有聽過,快說給我聽吧!
秒是時間的單位,是國際單位制(SI)七個基本單位中的其中一個。它一般可以理解為一天的86400分之一。
是的,一天有86400秒,只需要把60秒 x 60分鐘 x 24小時便可以計算出來。
然而,對於時鐘的每一滴答聲就是一秒,你可知道其間隔是如何定義的嗎?
我猜科學家可以運用一些儀器去測量一年裡的總秒數,然後再與自己的時鐘作比對。
用數量比對這個方法是個好主意,但應該不容易實行,你知道為什麼嗎?
這種方法似乎不容易實行,因為我們需要用很長的時間去收集時間數據。此外,老師曾經告訴過我,地球的自轉速度是不穩定的。
不錯。這就是爲什麽科學家有時候需要增加閏秒。最近因爲2021年地球自轉的速度加快了,有消息稱科學家正在辯論應否增加負閏秒以作補償。因此,我們並沒有一個恆定的參考去作比對。你認為還有哪些其他的方法可以使用?
我想就像用來測量長度的間尺一樣,我們可以通過使用更精細的間尺來提高準確性。同樣原理,我們可以使用一個較精準的時間標度來定義一秒的間隔。如果有非常穩定並且比一秒鐘要運轉得更快的機器,可能會有用。
這是個好方法!隨著量子力學的發展,科學家們不再將時間與地球的移動作比對,而是與某種原子的頻率作比對。即以天文觀測來測量時間的方法已經被監測頻率的方法所取代。
那麼我們如何將時間與原子的頻率聯繫起來?
我們是使用原子鐘。國際原子時(TAI)是通過全球約400台原子鐘來建立的參考時間。
香港有原子鐘嗎?
(笑)我們當然有。在我工作的實驗室裡便有兩套銫原子鐘用作香港的頻率標準。我曾經負責操作它們。讓我給你看張照片。

哇!真棒!。我想了解更多。甚麼是原子鐘,以及如何用它去定義秒?
我先給你正式答案。看看你能否理解。
1967年,國際計量局(BIPM)選擇了銫133原子來定義秒這個單位。秒的定義最近於2019年5月20日修訂為:
國際單位制的時間定義為秒,該單位符號為s。它是通過銫頻率的固定數值來定義。銫頻率指銫133原子在不受干擾基態的超精細能階躍遷頻率,頻率值為9 192 631 770 Hz。單位Hz等同於s−1。
我一個字都聽不懂!
不用擔心,當你長大後並在大學裏學習理科時便會了解它們。
但我現在便想了解它。您能以最簡單的方式來解釋給我聽嗎?
好的。那讓我試試吧。
什麼是銫?
銫是一種在28.5°C時即熔化的金屬,帶銀金色。將它放入水中會爆炸。因此,它是一種危險的物質。
那當您操作銫原子鐘時,會發生爆炸嗎?我很擔心您有危險啊......
放心吧,沒問題的。原子鐘僅儲存極少量的銫,並且被密封在管中,與水份隔絕。
銫133中133這數字是什麼意思?
一個原子是由三種類型的基本粒子組成,名為電子,質子和中子。質子和中子的總數稱為原子的質量數。銫原子具有55個質子和55電子,但可能具有不同數量的中子。銫133是一種具有78個中子的銫原子。質量數為55 + 78 = 133。
我知道什麼是電子,質子和中子。我最近讀了一本關於科學的書。它說電子,質子和中子是帶有負,正,及無電荷的微小顆粒。它也說質子和中子位於原子的原子核中心,電子在原子核周圍移動。不同的原子具有不同數量的電子,質子和中子。世界上的一切都是由原子組成的!
非常好!我都不知道原來你已經認識那麼多東西。你確實講得對的。我把它畫在電子黑板上......
外圍的電子和中間的原子核看起來就像圍繞著地球旋轉的月亮一樣。
我在這張圖中只簡單地畫了一個點去表達那55粒電子。實際情況有點複雜,但暫時可以先用這種方式去理解。
銫原子具有55個電子。這意味著有55顆月亮。我無法想像它們是如何分佈的?
你可以想像它們像土星環那樣分佈。土星環由幾層環組成。每層由不同數量的彗星,小行星或破碎的衛星組成。 銫原子或其他原子的電子分佈與此相似。
銫有六層電子,在量子物理學中,這些層通常稱為能級(n),每個能級具有不同數量的電子。讓我在黑板上畫出電子的分佈。在其最外層只有一粒電子。

這些電子可以從一個能級移動到另一個能級嗎?
他們是可以移動的。
如果電子從高能量的能級移動到較低能量的能級,則會發射一種稱為光子的粒子。
我們可以看到光子發出的光嗎?
這取決於光子的頻率。頻率是指振盪速率。
因此,您提到的9 192 631 770 Hz是光子的頻率。
正是!
我們可以看到頻率為9 192 631 770 Hz的光子嗎?
我們看不到。因頻率太低,超出了我們眼睛的可見範圍。但是我們可以使用電子電路來偵測。就像我們在原子鐘中使用的電路。
什麼決定光子的頻率?
這取決於兩個能階之間的差異。我們可以使用這個方程式進行計算。h是普朗克常數。普朗克是一位非常聰明的科學家。他於1918年獲得諾貝爾物理學獎。
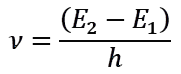
如果9 192 631 770 Hz是低頻,這是否意味著從E2躍遷到E1之間的能量差很小?
是的,這就是為什麼我們稱這個跳躍為超精細能階躍遷。
我記得您在兩年前繪製了一個具有許多水平綫的圖表。您非常喜歡該圖並將這幅圖貼在書檯上。它與超精細能階躍遷有關嗎?
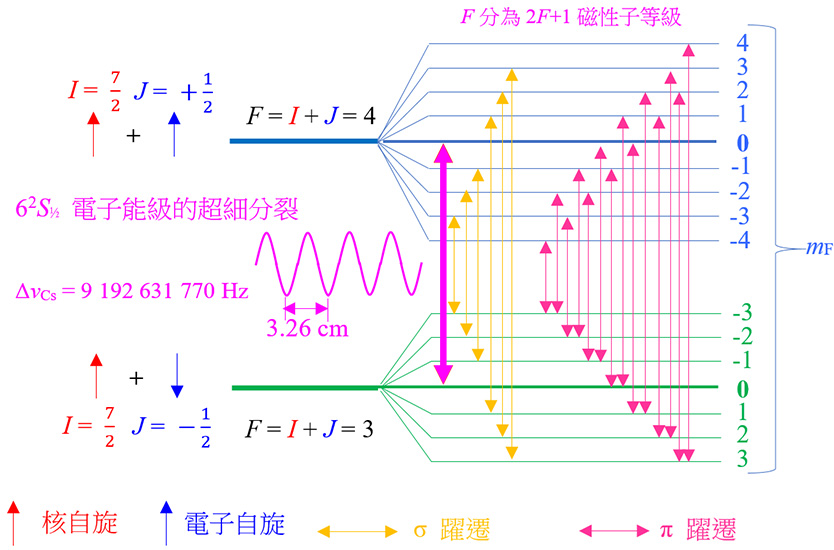
是的。我剛告訴過你,我曾經負責操作銫原子鐘用作香港的頻率標準,所以我需要了解這幅圖。
看起來超酷,可以解釋給我聽嗎?
不,那太困難了。
什麼是F?
...
什麼是mF?為什麼mF有這麼多的層級?
...
您經常教我:“羅馬不是一天建成的,學習亦然。知識是要終身努力才能獲得的東西。”我目前可能不瞭解的東西,說不定能啟發我......
快說吧!
那好吧,讓我試試看能不能使你明白。F是我們稱為Cs-133原子的總角動量。
總角動量!感覺是那麼拗口。
這個概念實際上很簡單。你知道什麼是陀螺吧。它會旋轉。電子,質子和中子都像陀螺一樣旋轉。角動量是量度這些粒子自旋的速度。對於電子,質子和中子,它們的角動量只有兩個值,即+1/2或-1/2。我們通常稱它們的角動量為自旋。
那麽,電子不能具有其他值的角動量嗎,例如0或1.23?
不,電子,質子和中子的角動量只能有離散而不連續的值。這就是為什麼我們稱這門科學為量子物理學。
為什麼角動量有這樣的特性?
大自然就是這樣,沒有人知道原因,甚至連愛因斯坦也不知道為何這樣。
說到總角動量,是否F等於所有55個電子,55個質子和78個中子的角動量加 在一起?
從某種意義上來說是對的。幸運的是,大多數電子,質子和中子都是成對並以相反的自旋而存在的,從而彼此抵消。因此,我們可以簡化一個Cs-133原子的總角動量F取決於最外層電子在n = 6能階下的自旋J和原子核的自旋I。
那麼F = I + J?
類似這樣。在量子物理學中,我們用一條特殊的規則將兩個自旋加在一起。J的值為1/2,I的值為7/2。視乎最外層電子與核的自旋的相對方向,總自旋F可以等於|I – J| ,即是3,或|I + J|即是4。
F = 3和F = 4就是那兩個超精細能階嗎?
正確的!你真聰明。
為什麼兩個超精細能階具有不同的能量?
我們可以想像電子和原子核為極微小的磁石。兩個超精細能階對應於兩個磁體是否指向相同的方向,我把它們畫在黑板上。你認為代表電子的磁石較容易停留在F = 3的狀態還是F = 4的狀態?

我的老師教過我,磁石的北極會吸引南極,並排斥另一個磁石的北極。因此,我認為保持F = 3狀態會更容易。
對,我們需要額外的能量才能使原子從F = 3狀態變為F = 4狀態,因此,他們之間存在一個能隙。
為什麼我們稱其為超精細躍遷?有“不精細躍遷”嗎?
F = 3和F = 4狀態之間的能量差非常小,因為原子核的磁場遠弱於電子的磁場。
為什麼原子核的磁場會是弱的?
這是因為組成原子核的質子和中子的質量比電子大得多,而粒子的磁場與其質量成反比。你只能相信我所說的,因為我現時無法告訴你大自然為何會有這種現象。
為什麼會有這麼多的mF層級?
我先前已經說過,電子,質子和中子是極微小的磁石。如果對Cs-133原子施加外在磁場,則不同方向的磁體將具有不同的能量。結果,能量層級將被再進一步分割。
在F = 4,我發現mF有9個水平。
是的,磁場會將F的超精細能階劃分為(2F + 1)個子能級
當F = 3時,(2F + 1)等於7,所以我們有7個子級別。
正確的!
因此,在F = 4的9個子層級中的任何一個都可以轉換到F = 3的7個子層級,那麼我們不是有很多不同的躍遷嗎?而每個躍遷可以產生不同的頻率嗎?
在原子鐘中,我們僅利用從(F = 4,mF = 0)到(F = 3,mF = 0)的躍遷。如圖上的標記。
這就是產生9 192 631 770 Hz頻率的超精細躍遷嗎?
是的,總而言之,超精細結構是由從電子運動和核自旋的磁場相互作用引起。
現在,我學會了很多有關銫-133原子超精細能階躍遷的東西。我還有一個問題,我們花了很多精力來定義秒,並設計了一套非常複雜的系統。其實,為什麼我們需要有一個這麼高精度的時鐘呢?對於一般人來說,這種準確度未必是必需的?
我想很多人可能有同樣的問題。但是,在人類歷史上,有很多例子表明了更精確的測量將可以促進科學技術的突破性發展。就讓我舉一個例子。在19世紀,阿爾伯特·邁克爾遜改善了他的干涉儀設計,能非常精準地測量光的速度,幷證明了光速是恆定的。結果成爲推動愛因斯坦發展相對論的重要理據。
原來如此。
下圖顯示了國際單位制(SI)基本單位之間的關係。可以看出,除了基本單位摩爾(mol)之外,另外的5個基本單位都取決於秒。如果我們可以提高時間的精度,那麼另外5個SI基本單位的精度都能受惠。
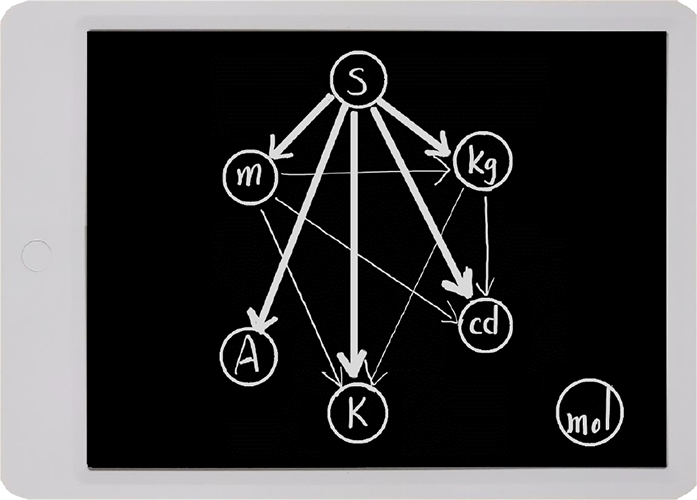
在推動使用銫133定義時間的SI基本單位中,誰的貢獻最大?是我的榜樣愛因斯坦嗎?
阿爾伯特·愛因斯坦以他的狹義相對論和廣義相對論徹底改變了物理學。他是一位偉大的科學家,但是還有許多人為現代科學做出貢獻的,包括楊格,馬克士威,赫茲,波利,米歇爾森,普朗克等。
就像足球隊一樣,球隊中的每一個人,包括球員,教練,醫療隊等,都必須共同努力才能成功。
希望有一天我也能為科學發展作出貢獻。
我很高興聽到你這樣說。
已經晚上11:30,你們兩個還在說甚麼!明天還需要早起上學和上班!
這個故事很有趣,我還不想睡覺。
哦,明天可以繼續。
我們明天繼續故事吧。
好的,晚安!
對於電子自旋,我在想一些事情。
那是什麼?
潛行兇間......
大聲笑......讓我們進入我們的潛意識。
(在爸爸的腦海中......十年後我們的對話將會如何?他將來會學習科學和工程嗎?讓我寫一封關於量子物理學的信讓他十年後看......)
Zzz.................
(待續)
測温學
温度的物理意義是否真的艱深到難以理解?

標準及校正實驗所
温度實驗所
林凱珊 張志培
温度並不簡單
温度影響我們的日常生活,人人皆知温度與冷暖的感受有關,卻鮮有人會思考其物理意義。
思考過這個問題的人會發現,温度與熱力學第二定律有密切連繫。因此,國際單位制(SI) 便特別為這個物理量採用「熱力學温度」一詞。為簡單起見,本文餘下部分將以「温度」指稱「熱力學温度」。
在七個國際單位制基本單位所代表的量中,温度的物理意義被指是最難理解的,就讓我們看看能否推翻這種說法。
温度的最簡單定義
温度應該是這樣的一個量,能量總是會從高温的地方流向低温的地方。當兩個物體進行熱接觸時,如果沒有發生能量流動,便即是兩個物體處於相同温度。這就是温度的最基本定義。
可惜,這個定義沒有太大用處。要理解温度的意義,需更詳細研究能量和統計理論。
温度與能量之間的緊密聯繫
2019年出版的《國際單位制手冊》第九版指出:「波玆曼常數k是對應温度(單位:開爾文)和能量(單位:焦耳)的量之間的換算系數,……」
及
「一個系統的温度與熱能成比例關係,但對系統的內部能量卻並不一定有此必然關係。」
顯然,温度與能量密切相關。究竟兩者之間的關係為何?
温度只是能量的別稱嗎?
假設有一個氣體樣本,其質量等於m、能量等於U、體積等於V、温度等於T,而壓力等於P。如果加入一個相同的樣本,合併後的氣體樣本會有以下屬性:質量等於2m、能量等於2U、體積等於2V、温度等於T,而壓力等於P。
| 氣體樣本1 | 氣體樣本2 |  |
合併後的氣體樣本 |
|---|---|---|---|
|
質量 = m 能量 = U 體積 = V 温度 = T 壓力 = P |
質量 = m 能量 = U 體積 = V 温度 = T 壓力 = P |
質量 = 2m 能量 = 2U 體積 = 2V 温度 = T 壓力 = P |
由此可見,質量、能量和體積的數值與系統大小成正比,稱為廣延量;反觀温度和壓力的數值則不受系統大小影響,稱為强度量。强度量通常是兩個廣延量之間的比例。
顯而易見,廣延量不能同時也是强度量,因此温度與能量並不相同。
那麼把温度定義為系統中的粒子平均動能又如何?
由於粒子(如分子或原子)的平均動能屬强度量,因此這種定義較為可取。事實上,物理學入門課程亦常以此解釋温度的物理意義。
就單原子組成的理想氣體而言,其內在能量包含原子平移運動的動能。當U是內部能量、N是粒子數目、k是波玆曼常數,而T是温度時,我們可以得出以下結果:
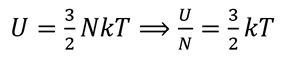 (1)
(1)
這個結果顯示温度與單個原子的平均動能(U/N)構成直接關係。
然而,當涉及雙原子氣體、液體和固體時,情況就變得複雜。除平移運動的動能外,這些物質的內部能量形式還包括轉動能、振動能和勢能。雖然以平均動能來解釋温度會較易理解,但這作為定義卻未如理想,因此需要一個更嚴謹和通用的定義。
大多數熱物理學教科書如何定義温度?
在大多數熱物理學教科書中,温度的定義如下:
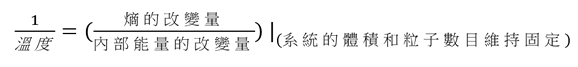 (2)
(2)
從字面上看,温度是熵的改變量除以內部能量的改變量的倒數,而系統的體積和粒子數目則維持於固定值。
為準確表達科學概念,物理科學的教科書常常載有使用微積分符號的數學方程式,例如温度(T)的定義通常以下列方程式表示:
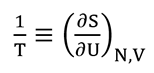 (3)
(3)
其中T是温度、S是熵、U是系統的內部能量、V是體積,而N是系統的粒子數目。
即使沒有讀過微積分,這道方程式也不像看起來般難解。如果把熵(S)與系統的內部能量(U)繪製成圖,偏微分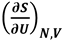 僅為曲線的斜率,而系統的體積(V)和粒子數目(N)維持固定。温度是該斜率的倒數。
僅為曲線的斜率,而系統的體積(V)和粒子數目(N)維持固定。温度是該斜率的倒數。
這道方程式看似簡單,但難處固然在於理解熵的意義。十九世紀的科學家便花了數十年時間才能解讀其意義,而這亦是很多人認為温度的物理意義難以理解的主要原因。不過,在統計力學領域的科學家們成功闡明熵的性質至今已逾百年。只要有一點耐心,我們定能理解熵的本質。
甚麼是熵?
1877年,路德維希.波茲曼(Ludwig Boltzmann)對熵作出以下定義:
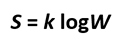 (4)
(4)
當中S是熵、k是波茲曼常數,W(多重度)是系統可及的量子狀態的數目。這是熱物理學其中一道最著名的方程式,鐫刻在波茲曼的墓碑上。
要理解這道方程式,我們需要知道甚麼是宏觀狀態和微觀狀態。一個系統的宏觀狀態是指其宏觀性質,例如温度和壓力;微觀狀態則指系統在特定時刻的具體微觀排列。
每個宏觀狀態都存在很多個會演化成相同宏觀狀態的微觀狀態,稱為宏觀狀態的多重度。多重度的對數就是熵。
統計力學的基本假設是在處於熱平衡的孤立系統中,所有可及的微觀狀態出現的機率均相等。因此,如有兩個宏觀狀態,其中微觀狀態數量較多(即多重度較高)的一個宏觀狀態出現的機率會較高。
同樣地,當孤立系統趨向熱平衡時,便很可能是處於微觀狀態數量最多的宏觀狀態,即最大的熵;當孤立系統遠離熱平衡時,則很可能會朝著熵較大的宏觀狀態演化。換言之,熵總是會增加。這就是著名的「熱力學第二定律」。
為對多重度這個重要概念有個大概認識,讓我們一起看看一個在攝氏23度及1標準氣壓的0.001立方米氦氣的樣本:當中由「薩克爾-泰特洛德(Sackur-Tetrode)方程式」計算出來的熵(S)是5.15 JK-1,微觀狀態的數目(W)是e3.73x1023。這個數字十分龐大,一般計算機進行運算時會出現溢位。
單原子理想氣體系統的熵可用薩克爾-泰特洛德(Sackur-Tetrode)方程式計算得出。這道方程式約源於1912年,由薩克爾 (Otto Sackur)和泰特洛德 (Hugo Martin Tetrode)各自提出。
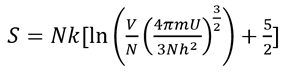 (5)
(5)
當中
N是原子數目、V是系統容量、m是原子體積、U是系統的內部能量,而h是普朗克常數。
熵、温度與能量流動的方向
以下內容結合熵的概念和統計力學的基本假設,解釋為何以方程式(3)定義温度會得出能量總是從高温地方流向低温地方的預期結果。以下內容,即使沒有學過微積分也能理解。要透徹理解的話要多花一點點功夫,但卻饒有裨益。
假設兩個系統處於熱接觸狀態,其內部能量分別為U1和U2,而w1(U1)和w2(U2)是這兩個系統分別可及的微觀狀態數目。兩個系統合併後可及的微觀狀態總數wc(U1, U2)如下:
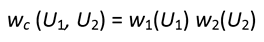 (6)
(6)
我們早前已定義熵(S)為S = k log w。在方程式的左右兩方取對數。
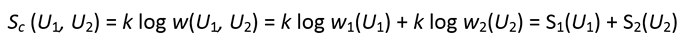 (7)
(7)
方程式顯示熵屬廣延量。系統合併後的總能量(Uc)等於U1 + U2。在孤立的系統中,Uc是守恒不變的。由於Sc(U1, U2) = S1(U1) + S2(Uc - U1),因此Sc(U1, U2)可以簡化為Sc(U1).
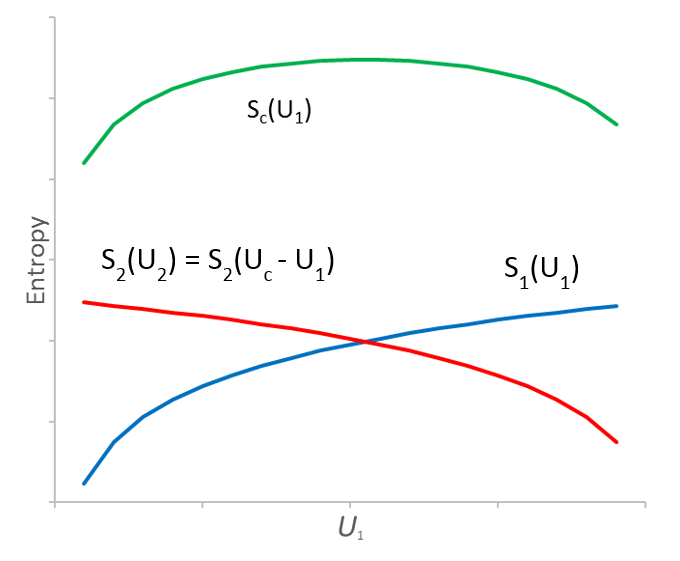 圖1 兩個處於熱接觸的系統因能量流動而令熵有所改變
圖1 兩個處於熱接觸的系統因能量流動而令熵有所改變
當能量ΔU從系統1流向系統2,U1便會減少ΔU,而U2會增加ΔU,Sc(U1)的數值亦會有所改變。這些數量的關係顯示在圖1。根據統計力學的基本假設,ΔU會向wc(U1, U2)和Sc(U1)數值增加的方向流動,因此,Sc(U1)的變化(以ΔSc(U1)表示)會大過或等於零。ΔSc(U1)可利用以下算式計算:
 (8)
(8)
讓我們以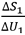 表示S1(U1)與U1的變率,則
表示S1(U1)與U1的變率,則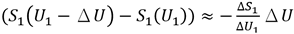 。同樣地,
。同樣地,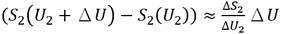 。ΔSc(U1)可簡化成:
。ΔSc(U1)可簡化成:
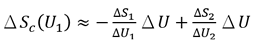 (9)
(9)
由於ΔSc(U1) ≥ 0,如果ΔU > 0(即能量從系統1流向系統2),我們便會得出:
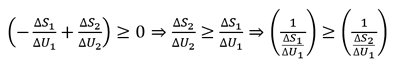 (10)
(10)
因此,以熵(S)相對於內部能量(U)變率的倒數來定義温度,與能量總是從高温地方流向低温地方的預期結果是一致的
希望藉此簡介,大家可以更加了解温度和熵的物理意義。
以下討論內容專供懂得微積分的人士閱讀。
合併系統的總能量為Uc = U1 + U2。總能量Uc維持不變。當兩個系統之間發生能量流動,便可得出dU1 = -dU2。
合併系統的可及微觀狀態總數可從下列等式得出:
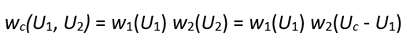 (11)
(11)
根據統計力學的基本假設,U1和U2數值的轉變方向會令wc(U1, U2)傾向增加,即dwc ≥ 0。
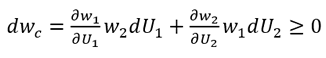 (12)
(12)
由於dU1 = -dU2,便可得出
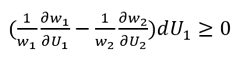 (13)
(13)
使用恆等式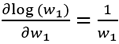 後,便可得出
後,便可得出
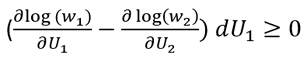 (14)
(14)
由於熵為S = k log w,便可得出
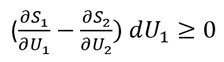 (15)
(15)
如果dU1 < 0(即能量從系統1流向系統2),便可得出
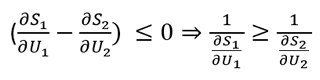 (16)
(16)
因此,方程式(3)所界定的温度符合能量從温度較高的系統流向温度較低的系統的預期。
感受水蒸氣

標準及校正實驗所
濕度實驗所
李河堂 林凱珊
1) 感受水蒸氣
夏季的相對濕度可以高達90 %RH 以上,我們置身在這種悶熱潮濕的環境裡,可能還會感受到身邊無形的水蒸氣呢! 你會否想過,我們只要透過一個簡單的實驗便能令這些無形的水蒸氣變得清晰可見呢?若你佩戴眼鏡,可能你已經從日常生活當中輕易取得答案。夏天時,當你從冷氣房間走到戶外,空氣中的水蒸氣會在冰冷的鏡片上凝結成無數的小水珠,令眼鏡表面起霧。這種水蒸氣的凝結現象看似普通不過,但箇中的物理學原理卻是準確測量相對濕度的基礎之一。
 圖1. 在冰冷鏡片上的凝結的水珠
圖1. 在冰冷鏡片上的凝結的水珠
2) 何謂相對濕度?
濕度是氣體的水蒸氣含量。濕度測量學是一門研究如何準確量度濕度的科學。它會透過不同方式來量化空氣中的濕度,例如相對濕度、露點温度,以及水蒸氣的摩爾分數或質量分數,當中以相對濕度最為常用。
空氣能容納有限的水蒸氣,其最大容量是以飽和水蒸氣壓ew(t)[單位:千帕斯卡(kPa)]來定義,即圖2中以温度t為函數改變的飽和線。相對濕度[單位:%RH]就是以飽和水蒸氣壓的百分比來表示的水蒸氣壓水平,如圖 2中顯示的10 %RH和50 %RH相對濕度的水蒸氣壓線。當水蒸氣壓達到飽和水蒸氣壓的水平,相對濕度便會達到100 %RH,而空氣中的水蒸氣就會凝結成露珠(即水珠)。
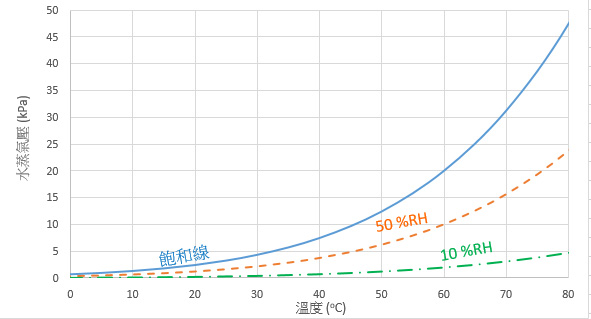 圖2.在不同温度下的飽和水蒸氣壓以及在50 %RH和10 %RH情況下的水蒸氣壓(假設氣體處於理想氣體的狀況)
圖2.在不同温度下的飽和水蒸氣壓以及在50 %RH和10 %RH情況下的水蒸氣壓(假設氣體處於理想氣體的狀況)
3) 相對濕度與露點温度的測量
水蒸氣的凝結現象,不僅是反映水蒸氣壓達至飽和的有效指標,還能用於釐定環境的相對濕度。以圖3為例,紅點是一個低於飽和點ew(60 °C)的未知空氣水蒸氣壓。如果把空氣的温度逐漸降低,其飽和水蒸氣壓會隨着飽和線下降。假如水蒸氣的含量固定不變,水蒸氣壓在整個冷卻過程便會維持不變。當空氣的温度降至td,飽和水蒸氣壓ew(td)會相等於水蒸氣壓的現有水平,而水氣便會在飽和的狀態下凝結成露珠。凝結出現時的温度稱為露點温度td,如圖3例子中的露點温度為45.8 °C。假設空氣處於理想氣體的狀況下,我們可以運用以下方程式計算空氣在60 °C時的相對濕度:
相對濕度 = 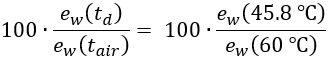
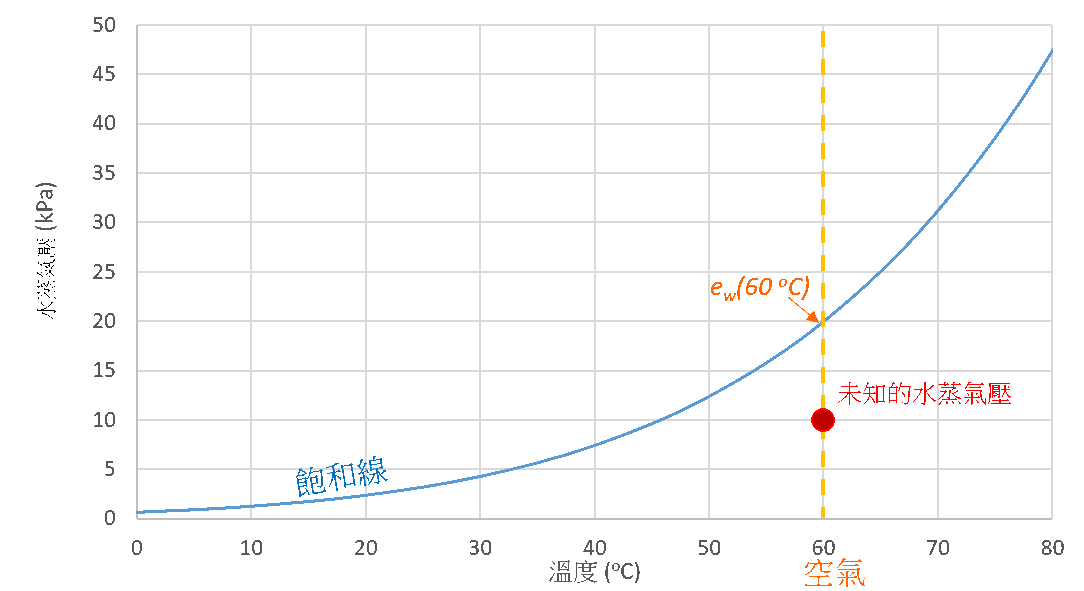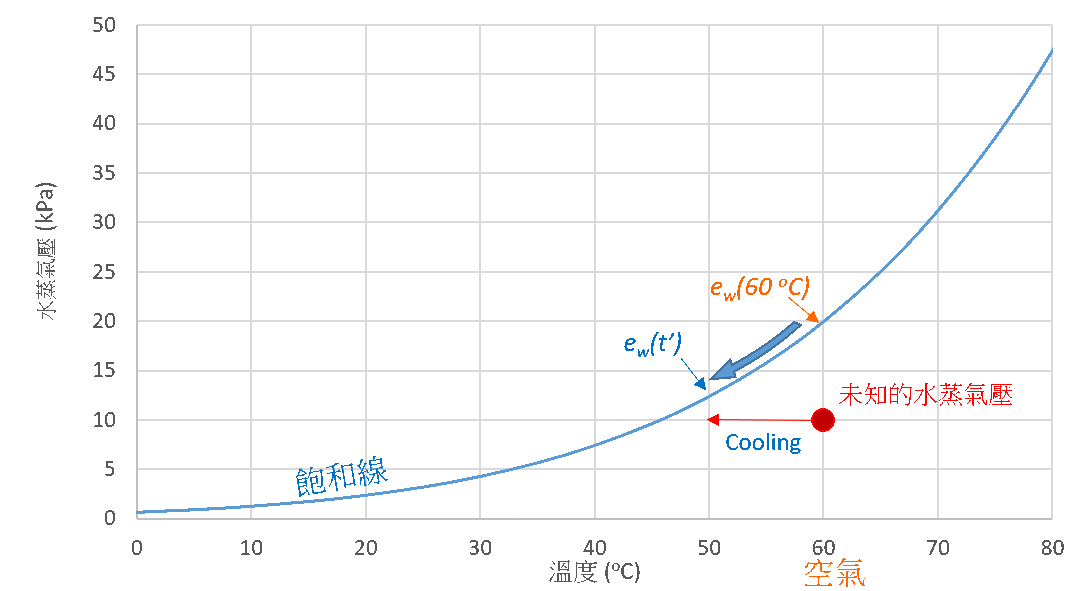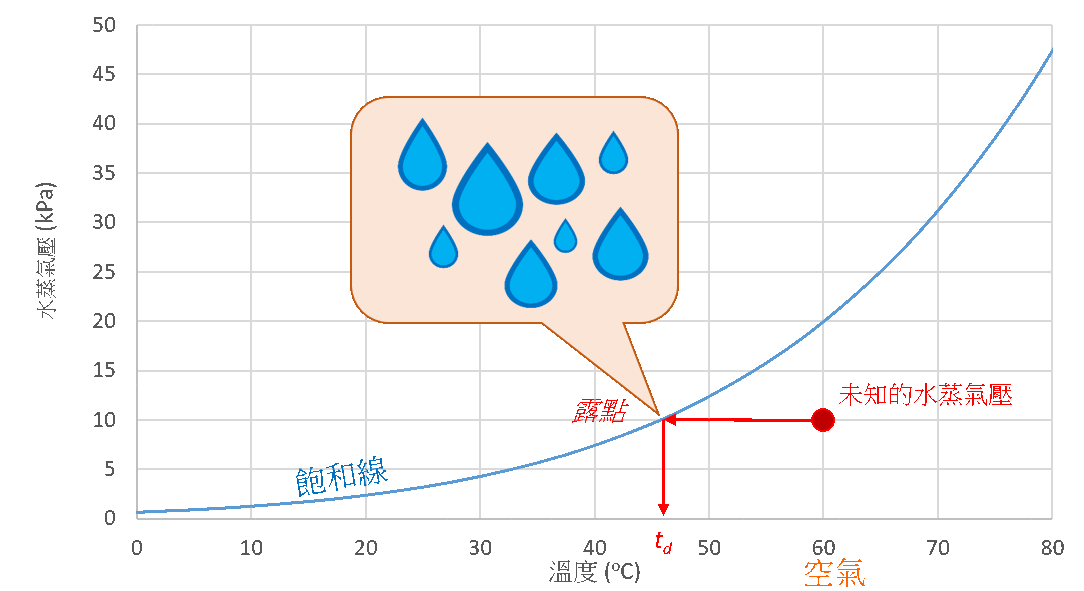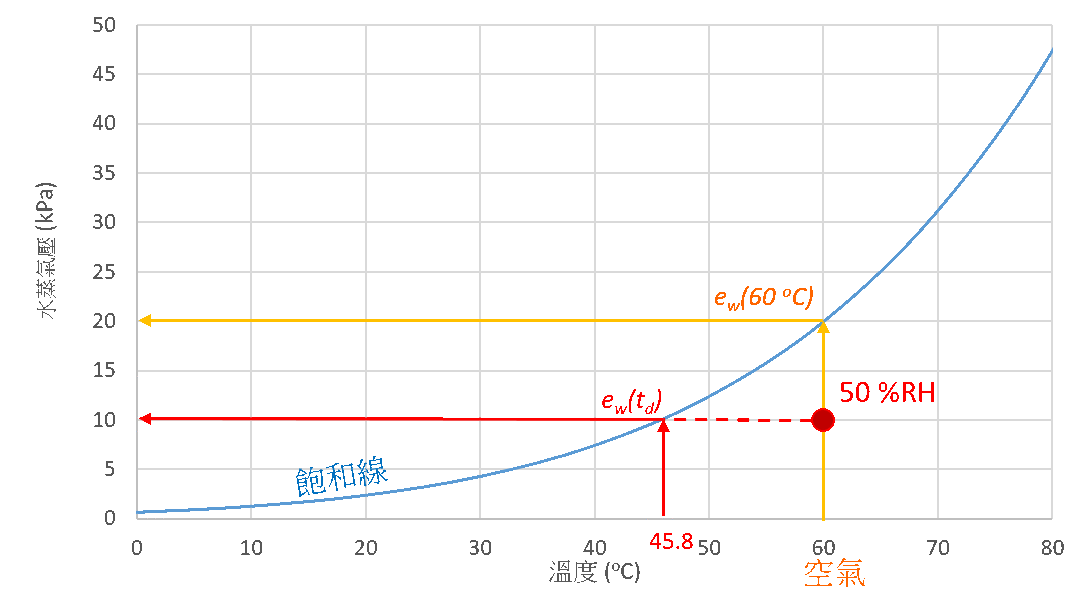 圖3. 用於估算相對濕度的露點温度
圖3. 用於估算相對濕度的露點温度
4) 鏡面冷凝式露點濕度計
鏡面冷凝式露點濕度計是利用凝結現象來準確測量露點温度的儀器。儀器露點温度的測量不確定度通常少於0.1 °C,相當於在室温下的不確定度為0.6 %RH以下。這部儀器包括一面高度拋光的鏡片(如圖4所示)。鏡片温度由一個多層的熱電冷卻器精準控制,並受一個內置的鉑電阻温度計監察。露點濕度計內的光學反饋系統由一個單色光源和數個監察光電探測器組成,用於探測凝結現象並穩定凝結狀態。圖5(a)的光電探測器1(PD1)負責監察來自鏡片的鏡面反射光,光電探測器2(PD2)則負責監察散射光線。當鏡片温度高於露點温度,來自光源的入射光便會被拋光鏡片反射至PD1,而PD2不會接收到任何光學訊號。當鏡片温度冷卻至露點温度,鏡片表面便會凝結出一層露珠(如圖5(b)所示),入射光會以不同角度散射,令鏡面反射光大幅減少。透過監察PD1和PD2分別接收到的反射光學訊號和散射光學訊號,便能探測水蒸氣的凝結程度。該反饋系統隨後會微調鏡片温度,直至凝結現象達到平衡狀態(即露珠既不增加也不蒸發)。最後,由鉑電阻温度計在平衡狀態下所測量的温度即為露點温度,用以計算相對濕度。
 (a)
(a)
 (b)
(b)
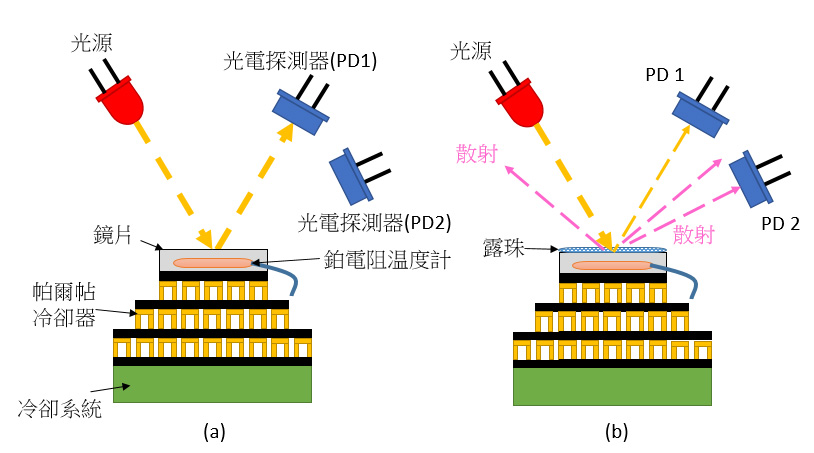 圖5. 用於測量露點温度的冷凝式鏡片探測器的常見結構。(a)和(b)分別為鏡片温度高於露點温度和相等於露點温度的情況
圖5. 用於測量露點温度的冷凝式鏡片探測器的常見結構。(a)和(b)分別為鏡片温度高於露點温度和相等於露點温度的情況
5) 其他常見的相對濕度測量儀器
市面上其他種類的相對濕度測量儀器甚多。我們會在本部分探討其中一些常見的儀器,例如乾濕球濕度計、電濕度計和機械濕度計。
5.1. 乾濕球濕度計
乾濕球濕度計由兩個温度計組成,一個用於量度空氣的温度(即乾球),另一個則封存於芯內,並利用儲水箱的毛細效應令芯內保持濕潤(即濕球)。芯內水分的蒸發速度隨著環境的濕度水平而改變,而水分的蒸發會使濕球得以冷卻。空氣的水蒸氣壓ew(td)數值可以運用下例方程式,從乾球(tdry)與濕球(twet)之間的温差計算出來:
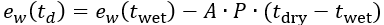
其中P代表大氣壓力,而A則代表乾濕計係數,典型值為0.00067。乾濕球濕度計可分為通風乾濕球濕度計和非通風乾濕球濕度計兩種。通風乾濕球濕度計內設有通風扇,提供恆定氣流,令測量結果較為準確。圖6為這兩種乾濕球濕度計的實物圖。乾濕球濕度計的測量不確定度一般約為2 %RH至5 %RH。


5.2. 電濕度計
電濕度計內的電阻式或電容式感應器以吸濕材料造成,並置於兩組電極之間。吸濕材料的電阻性或電容性會因應吸收的水量而改變。電阻式濕度計的吸濕材料可以是固定於兩根玻璃棒之間的液態電解質,而電容式濕度計的吸濕材料則可以是一層聚合物薄膜。為免受塵埃和污染物污染,感應器一般會封裝起來,如圖7的感應器實物圖片。電濕度計的測量不確定度一般約為2 %RH至3 %RH。當使用介電質材料時,濕度的升序和降序或會導致水分吸收率出現更為顯著的差異。這種差異在測量不同濕度的測試序列時或會造成遲滯誤差,宜多加注意。
 (a) 已封裝的電解電阻式感應器
(a) 已封裝的電解電阻式感應器
 (b) 電容式感應器的集成電路
(b) 電容式感應器的集成電路
5.3. 機械濕度計
機械濕度計是最早使用的濕度計。它量度物料在不同濕度下的膨脹和收縮程度來測量空氣中的濕度。感測物料有人類的毛髮、牛腸、紡織品或塑膠。如圖8所示,物料的尺度變化會以機械裝置(例如槓桿)放大至一支指針上顯示,並在移動圖表上作出記錄。機械濕度計的測量不確定度一般約為5 %RH至15 %RH。機械濕度計一般在室温下使用,它的反應時間緩慢,而遲滯誤差的問題亦更為明顯。
 (a) 機械濕度計
(a) 機械濕度計
 (b) 感測元件
(b) 感測元件
Reference:
- BS 1339-3:2004 Humidity. Part 3 - Guide to the measurement of humidity
- Handbook of temperature measurement, Robin E. Bentley
振動
智能電話精於偵測動態的玄機

區志豪, 林凱珊
聲學、超聲及振動實驗所
標準及校正實驗所
今時今日的智能電話設計精密,配備各式各樣的傳感器,例如加速度計、陀螺儀、磁強計、光照度計和輕觸式螢幕,能夠完成很多出色的工程任務。這些細小的機器能夠追蹤用家舉動、監測心跳和預測我們的需要,其中兩款最常用於智能電話的傳感器是加速度計和陀螺儀。
加速度計用於偵測電話的畫面方向,電話會因應擺放的角度從而轉換螢幕顯示的畫面方向,由直向轉為橫向,或由橫向轉為直向,為用家提供舒適的觀賞體驗。舉例來說,利用手提電話觀看YouTube影片的最佳模式是把電話水平放置,用家以橫向模式播放影片,影像不但能填滿整個畫面,而且更大更清晰。此外,加速度計亦可用作計步器,計算用家行走的步數。多種健康與健身和運動應用程式都會透過分析計步器計算的步數,判斷有關動作的頻率、強度、持續時間和模式,從而估算用家在運動期間消耗的卡路里,幫助他們記錄自己的運動常規以達到個人目標。一些較高端的電話會採用基于感應動作的姿勢識別演算法來分析三軸加速度計的輸出數據,以提升用家的流動應用程式和遊戲體驗。
不過,由於加速度計只能量度線性加速,它只可量度設備移動的方向;除非該加速度計同時配備陀螺儀或陀螺儀傳感器,否則便不能處理設備在移動期間向左右兩側傾斜的位置。陀螺儀是另一種用於智能電話的方向傳感器,用作量度角旋轉速率。陀螺儀通常會為加速度計收集的資料提供額外的維度,使加速度計能夠更準確地判斷電話的方向和移動情況。Google Sky Map和Pokemon Go等受歡迎的應用程式均使用陀螺儀數據來改善測量的準確度。
如今,最先進的九軸設備會將三軸陀螺儀、三軸加速度計和三軸指南針結合在同一塊晶片上,並加入數位運動處理器,用以實現各種複雜的移動演算法。
 圖1 iPhone 4內的意法半導體LIS331DLH加速度計和L3G4200D陀螺儀
圖1 iPhone 4內的意法半導體LIS331DLH加速度計和L3G4200D陀螺儀
加速度計的結構
加速度計通常裝有電子電路,利用電效應、壓電效應、壓阻效應或電容效應,探測裝置的輕微動作。現今用於智能電話的加速度計屬於微機電系統,採用微電子裝配技術裝配於矽基板上,成品體積極細。應用微機電系統的加速度計裝有一個微型的感震質量,連接於局限在固定金屬板之間循單一方向移動的彈簧系統。當該特定方向出現加速情況時,感震質量便會移動,而其與金屬板之間的電容亦會出現相應變化。電容變化與加速水平成正比,量度電容變化便可判斷裝置的移動情況。
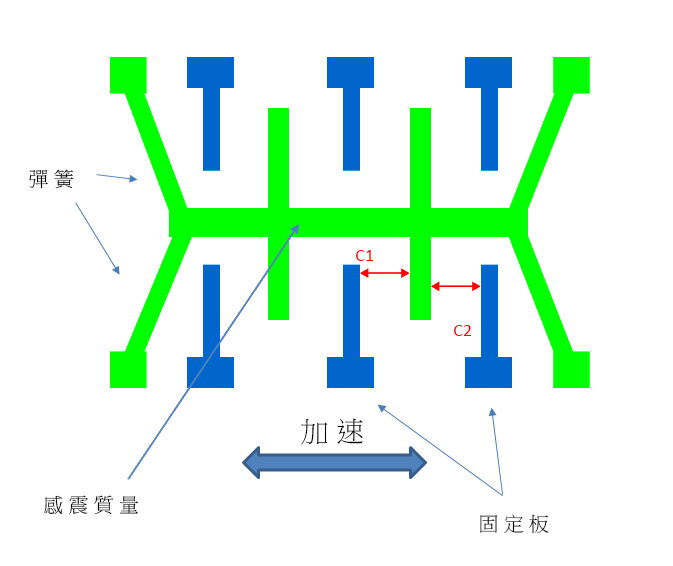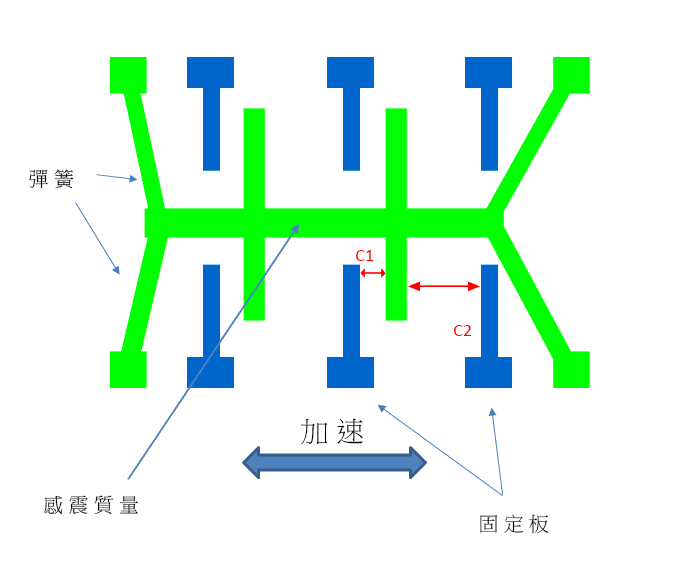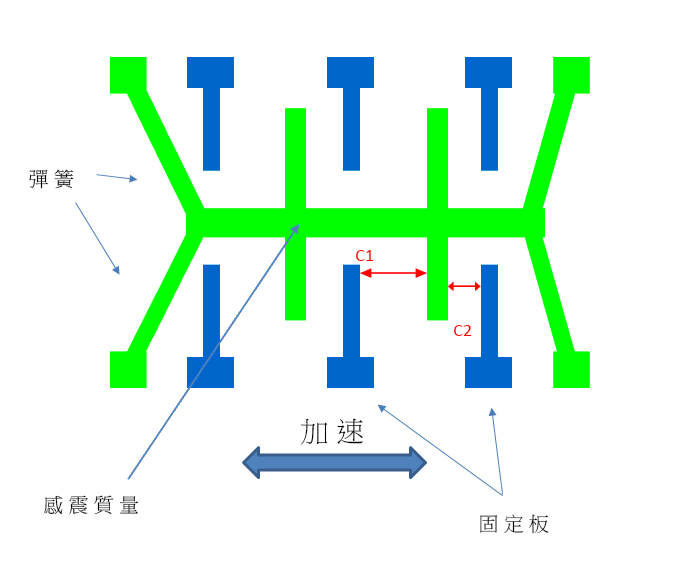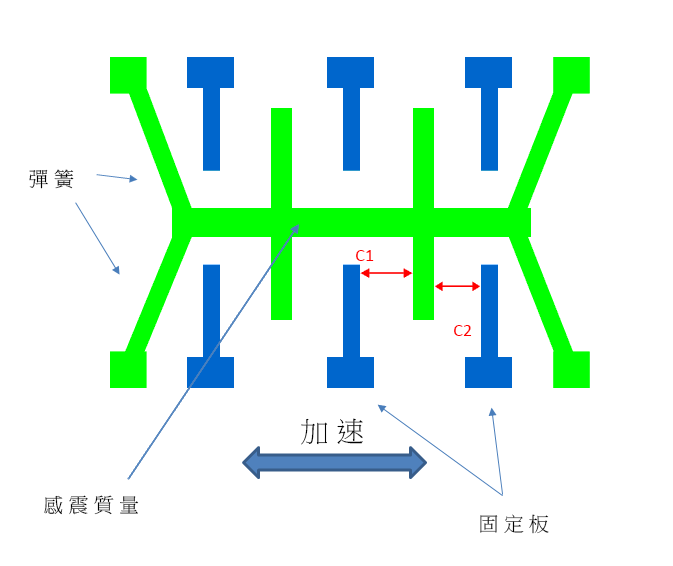 圖2 微機電系統加速度計內含感震質量的電路
圖2 微機電系統加速度計內含感震質量的電路
陀螺儀的構造
陀螺儀或陀螺儀傳感器是根據角動量守恆定律設計而成,用於量度或維持方向和角速。傳統的陀螺儀由轉輪或轉盤等轉子和外框組成,即使外框的轉動方向有變,轉子亦會維持旋轉軸的方向不變。
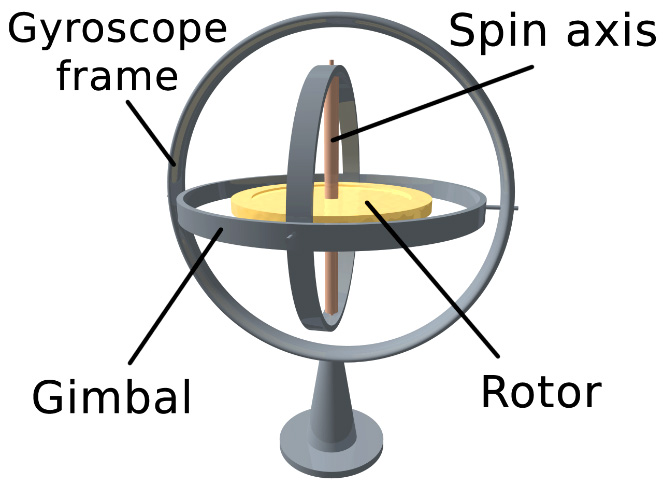
陀螺儀框架旋轉軸
平衡環架轉子
 圖4 傳統陀螺儀的運轉動畫(資料來源︰維基百科)
圖4 傳統陀螺儀的運轉動畫(資料來源︰維基百科)
不過,用於智能電話的微機電系統陀螺儀,則是根據另一項名為「科里奧利效應」(科氏效應)的運作原理設計而成。下圖解釋科氏效應的原理︰當某平台正在轉動,站在中心點附近的人向接近邊界的定點移動,其相對地面的切線速度便會如圖中的箭嘴長度所示而有所增加。因徑向速度改變導致切線速度出現的變化稱為「科氏加速」,量度科氏加速便可判斷角速。
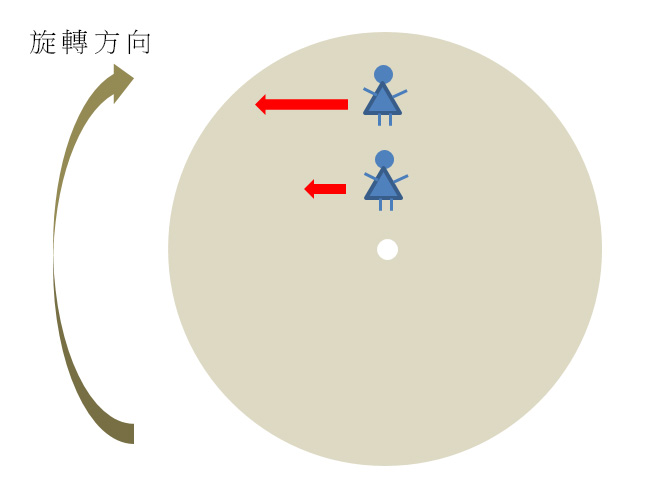 圖5 科氏效應概念圖
圖5 科氏效應概念圖
同樣地,當質量以特定速度向特定方向移動,由於科氏效應的影響,移動時外部角速率會令質量出現垂直位移。正如微機電系統加速度計一樣,位移亦會改變電容,量度電容變化便可判斷相應的角速率。
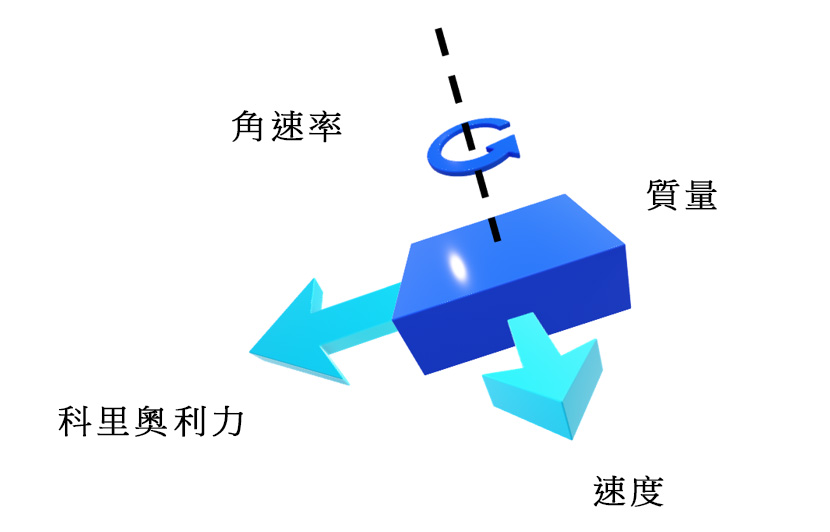 圖6 科里奧利效應的運動向量
圖6 科里奧利效應的運動向量
校正加速度計
一般方法
壓電加速度計一般是根據國際標準ISO 16063-21的背對背比較法進行校正。這個方法的基本原理是將接受測試的傳感器安裝在標準加速度計上,然後讓兩者同時達至相同的加速度。該傳感器的靈敏度可從兩者的電輸出信號之間的比率數值與標準加速度計的靈敏度得出。這個方法簡單易用,因而廣泛應用於常規的校正或性能檢查工作。
原級方法
參考標準加速度計或高精準度的工作級別加速度計,必須以原級方法進行校正。國際標準ISO 16063-11闡述了加速度計的各種原級校正方法。
方法一(條紋計數法)用於校正在1 Hz至800 Hz頻率範圍內的靈敏度幅值;方法二(極小點法)用於校正在800 Hz至10 kHz頻率範圍內的靈敏度幅值;方法三(正弦逼近法)用於校正在1 Hz至10 kHz頻率範圍內的幅值和相位靈敏度。
由於方法三涵蓋較廣的頻率和振幅範圍,亦能測量振動信號的振幅和相移,因此被廣泛應用於加速度計的原級校正。
標準及校正實驗所的原級振動測量系統
下圖為標準及校正實驗所的振動測量系統的主要儀器。該系統利用電動激振器產生動量。接受校正的加速度計安裝在激振器上,而激光振動計則安裝於振動隔離地基頂部,並以激光光束對準加速度計周圍的位置。該系統以激光干涉法的原理為基礎,採用波長為633納米的紅色氦氖激光。干涉儀的正交輸出信號及壓電加速度計經濾波和放大的電信號,會被數位示波器同時取樣,然後透過採用正弦逼近法的軟件處理相關的數碼資料,以計算出加速度計的複數靈敏度。
 圖7 標準及校正實驗所的振動測量系統
圖7 標準及校正實驗所的振動測量系統
利用激光干涉儀進行原級振動校正的操作原理
根據國際標準ISO 16063-11所載的方法三,可利用光學干涉法把機械位移、速度和加速度溯源至激光的波長。圖8是使用零差技術的改良版邁克生干涉儀的光學原理圖,所用激光是波長為633納米的穩頻氦氖紅光。
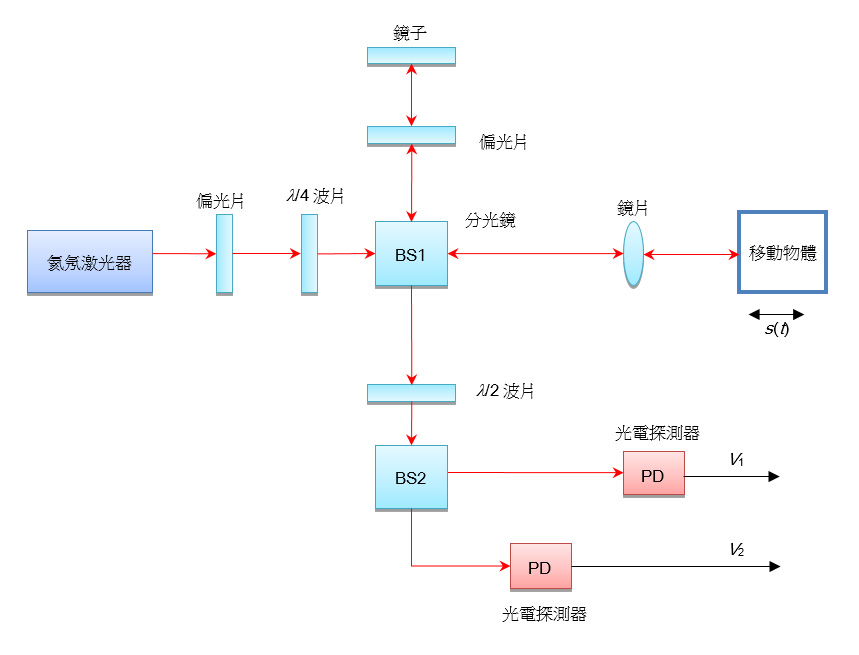 圖8 改良版邁克生干涉儀的原理圖
圖8 改良版邁克生干涉儀的原理圖
經偏振的激光光束通過λ/4波片後,變成圓形偏振光。非偏振分光鏡(BS1)把該入射光束分成兩道強度相等的正交光束。參照光束經偏振後射向一面固定的鏡子。圓形偏振的測量光束從一個移動物體的表面反射並回到BS1。參照光束和測量光束通過λ/2波片,該波片作調整後可令偏振分光鏡(BS2)產生光干涉,從而形成兩道分別對應於同相(I)和正交(Q)分量的兩個光束。光電探測器(V1)和(V2)的輸出電壓, 代表I和Q的數值. 按照下一節的計算方法, 可準確算出移動物體的位置. 加上采樣的時間, 就可算出移動物體的速度及加速度。
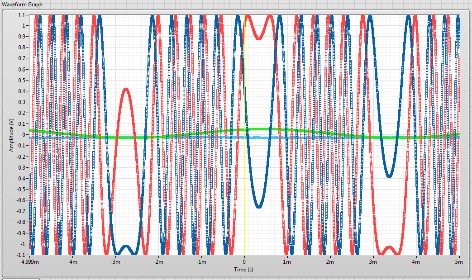 圖9 光電探測器(V1)和(V2)的輸出電壓
圖9 光電探測器(V1)和(V2)的輸出電壓
正弦逼近法的計算方法
此一節比較適合對數學有興趣的讀者。
光電探測器(V1)和(V2)的輸出電壓, 在去除直流分量后, 会按下列方程式,隨兩道光束之間的調制相位差ϕmod而變化。
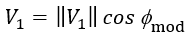 (1)
(1)
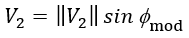 (2)
(2)
測量光束是從移動物體散射回來的,參照光束和測量光束之間的光程差L(t)是時間的函數。設定s(t)為該移動物體的位移,而∅s為起始位移相位。
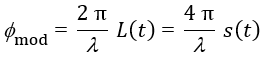 (3)
(3)
光電探測器和加速度計的輸出會同步取樣。國際標準ISO 16063-11所界定的正弦逼近法,可用作於數值正反切解調。假設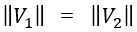 ,並以特定算法將相位展開,以避免因正反切函數的含糊性而出現不連續性。
,並以特定算法將相位展開,以避免因正反切函數的含糊性而出現不連續性。
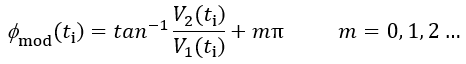 (4)
(4)
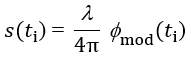 (5)
(5)
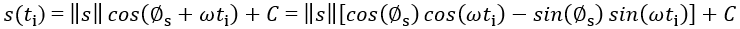 (6)
(6)
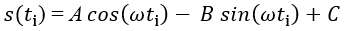 (7)
(7)
通過測量, 收集了n個不同調制相位差的數據。通過使用最小平方法求解n個方程,可以估算出A,B和C三個未知參數的數值。
以矩陣形式表示:
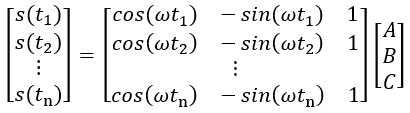 (8)
(8)
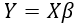 (9)
(9)
設定ϵ為誤差向量
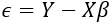 (10)
(10)
ϵϵT為平方誤差
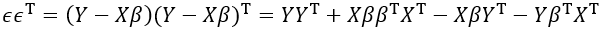 (11)
(11)
為了把平方誤差減至最小,設定有關β的期望值導數為零,即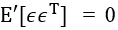 。
。
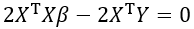 (12)
(12)
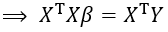 (13)
(13)
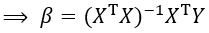 (14)
(14)
β是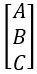 的最佳估計值。
的最佳估計值。
調制位移幅度為
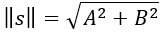 (15)
(15)
起始位移相位為
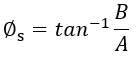 (16)
(16)
假設正弦振動頻率為ƒ、加速度值為a,而起始加速相位為∅a
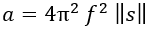 (17)
(17)
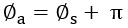 (18)
(18)
從加速度計同時取樣的一連串輸出數值u(ti),亦可運用正弦逼近法以同樣方式得出其約數
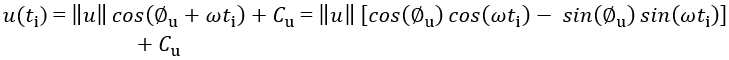 (19)
(19)
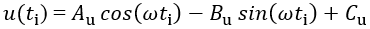 (20)
(20)
加速度計的輸出振幅為
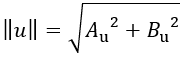 (21)
(21)
加速度計的起始輸出相位為
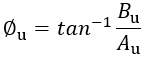 (22)
(22)
複數靈敏度的模數為Sa,而加速度計的相移為Δ∅
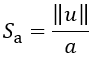 (23)
(23)
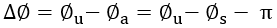 (24)
(24)
圖10顯示了計算的不同階段的數據。
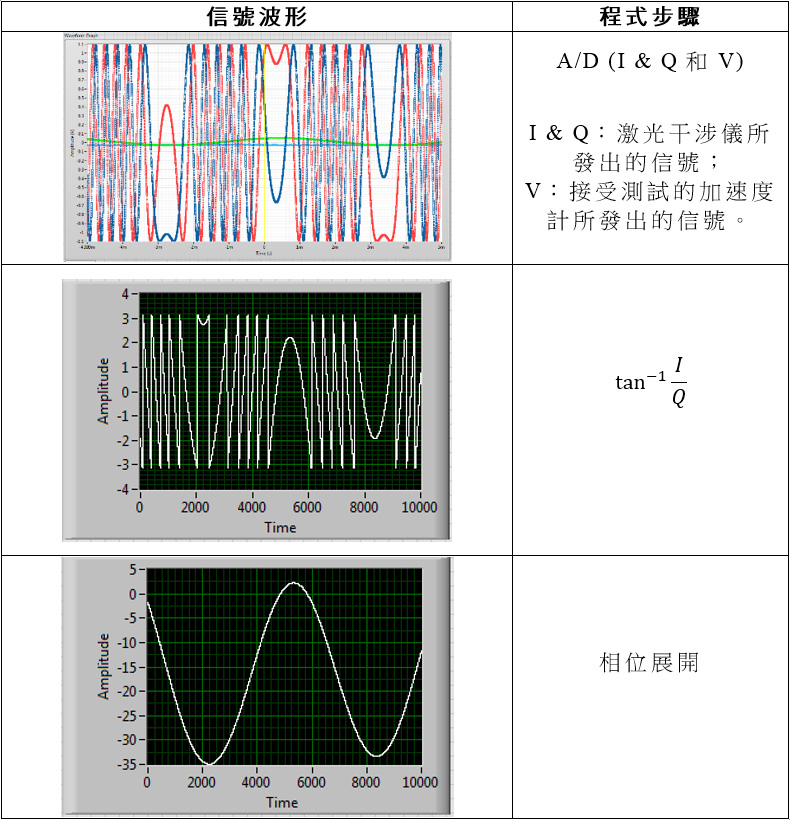 圖10 計算的不同階段的數據。
圖10 計算的不同階段的數據。
參考資料:
[1] ISO 16063-11:1999, “Methods for the calibration of vibration and shock transducers - Part 11: Primary vibration calibration by laser interferometry”
[2] ISO 16063-41:2011 “Methods for the calibration of vibration and shock transducers Part 41: Calibration of laser vibrometers”
[3] Primary vibration calibration with CS18P using laser vibrometer technology Holger Nicklich, Ume Buehn, SPEKTRA GmbH Dresden, Germany
[4] Realization and Results of a DKD Interlaboratory Comparison Regarding the Measurand Acceleration Dr. Thomas Bruns, Philipp Begoff, Michael Mende XX IMEKO World Congress Metrology for Green Growth September 9-14, 2012, Busan, Republic of Korea
[5] https://www.memsjournal.com/2010/12/motion-sensing-in-the-iphone-4-mems-accelerometer.html
[6] https://www.polytec.com/us/vibrometry/technology/
[7] HowToMechatronics.com